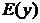 and Poisson ratio
and Poisson ratio 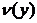 are the functions of the
are the functions of the 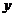 variable. The axis
variable. The axis 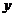 is directed downwards. The problem is to determine the stress-strain state of the band.
is directed downwards. The problem is to determine the stress-strain state of the band.Lamzyuk V.D., Hamhot’ko E.S., Atanova M.Y., Tsuladze A.O.
Oles Honchar Dnipropetrovsk National University, Ukraine
THE FIRST MAJOR PROBLEM FOR THE INHOMOGENEOUS BAND
The solution of boundary value problems of elasticity theory for layered objects has a great practical and theoretical significance. A lot of calculations of strength of largehydraulic structures, high buildings, mines, airport paving, roads, and designing composite structures make it necessary to solve problems associated with determination of the stress-strain state of multilayer environments.
We consider an infinite smooth band of inhomogeneous depth with the H thickness. The band is located in a plane deformation under external pressure that is applied to the outer boundaries of the band.
In this case Young's modulus 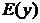 and Poisson ratio
and Poisson ratio 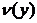 are the functions of the
are the functions of the 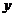 variable. The axis
variable. The axis 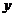 is directed downwards. The problem is to determine the stress-strain state of the band.
is directed downwards. The problem is to determine the stress-strain state of the band.
Mathematically, a plane problem of elasticity theory is reduced to solving the Lame system:
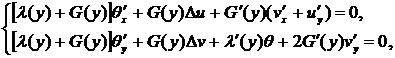 (1)
(1)
When Hooke's law is performed:
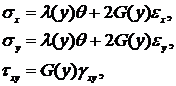 (2)
(2)
where
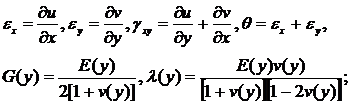 (3)
(3)
Boundary conditions are the following:
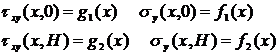 (4)
(4)
For the solution of the given problem the method of determination stress-strain state of inhomogeneous or multilayer band was constructed. This state occurs under externalpressure that is applied to the outer boundaries of the band. To this effect, the discretization band was performed in this work, which is approximately replaced by a multi-pack.
In this case within the each band (with 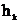 thickness) Young's modulus and Poisson’s ratio are the constant values, and for different bands, generally speaking, take thedifferent values. This problem of the multilayer package deformation was reviewed in [1].
thickness) Young's modulus and Poisson’s ratio are the constant values, and for different bands, generally speaking, take thedifferent values. This problem of the multilayer package deformation was reviewed in [1].
The limiting transition (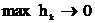 ) was made for the mathematical modeling of inhomogeneous planar deformation bands.
) was made for the mathematical modeling of inhomogeneous planar deformation bands.
We consider the deformation of inhomogeneous band under normal load specifically (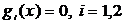 ).
).
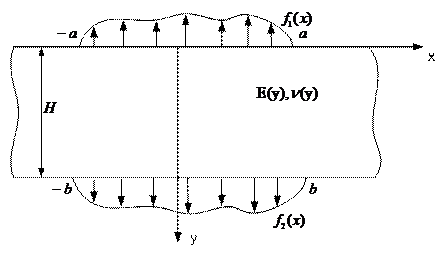
Figure 1. Endless smooth heterogeneous to the width band under flat strain
In this case boundary conditions have the form (see Figure 1):
 (5)
(5)
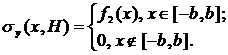 (6)
(6)
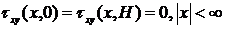 (7)
(7)
Let us break down the source band into 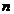 layers with the H thickness each. We assume Young’s modulus and Poisson’s ratio as piecewise-constant functions, constantwithin each layer
layers with the H thickness each. We assume Young’s modulus and Poisson’s ratio as piecewise-constant functions, constantwithin each layer 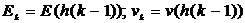 .
.
Let us numerate the layers from top to bottom 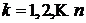 and take each layer to the local coordinate system
and take each layer to the local coordinate system 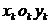 beginning from its upper limit and the axis
beginning from its upper limit and the axis  is directed into the middle of the
is directed into the middle of the  layer.
layer.
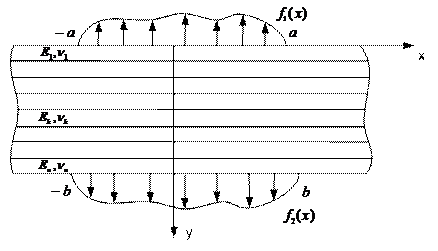
Figure 2. Discretization
Then the algorithm for solving the first fundamental problem (5) – (7) is the following:
1. By the ratios:
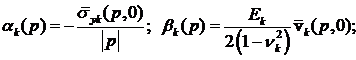 (8)
(8) 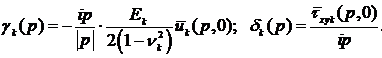
we determine the Fourier transforms:
 ;
; 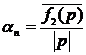 ;
; 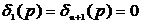 (9)
(9)
2. we find compliance function under the recurrent relations 
3. By the ratios:
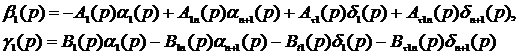 (10)
(10)
we get 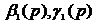 ;
;
4. From the recurrent relations given in the work we obtain four functions 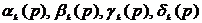 in a given layer;
in a given layer;
5. According to the formulas given in the work, we get the transforms of stress 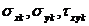 and displacement
and displacement 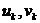 ;
;
6. Perform the inverse Fourier transform.
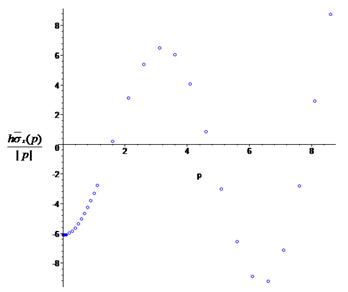
Figure 3. Graph transform strain 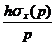
The software, based on the algorithm was implemented. It allows to calculate the Fourier transforms of the stress-strain state of inhomogeneous band.
We consider the strip with the thickness H = 1, the number of layers n = 3, the calculations are conducted in the second layer (k = 2), where Young's modulus 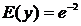 and Poisson’s ratio
and Poisson’s ratio  , y = 0,5.
, y = 0,5.
Literature:
1. Wolski S.L. Plane deformation of a multilayer board. Stability and strength of structural elements / S.L. Wolski, A.K. Privarnikov. – Issue 2. Dnepropetrovsk, 1975. – Р. 105-123.