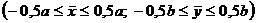 is hinged on
is hinged on 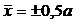 sides and on
sides and on 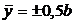 sides and has mixed boundary conditions of hinged-clamped type, symmetrical about the
sides and has mixed boundary conditions of hinged-clamped type, symmetrical about the  axis (Figure 1). Forcing pressure is applied to the plate:
axis (Figure 1). Forcing pressure is applied to the plate:Goncharenko D.S., Pasechnik V.A., Atanova M.Y.
Oles Honchar Dnipropetrovsk National University, Ukraine
RESEARCH ON FORCED OSCILLATIONS OF PLATES WITH MIXED BOUNDARY CONDITIONS
The usage of thin plates as supporting elements for constructions in many fields of modern industry makes the problem of analyzing and solving boundary problems of plate theory of great importance.
The boundary conditions of real-life constructions are often complicated and combine different types of support, clamping and hinging. These conditions may occur due to either project or the change of material’s properties during its lifetime.
The study of plate oscillations is reduced to solving fourth-order partial differential equations which satisfy corresponding boundary conditions. The exact solution of these problems can only be obtained for the several linear cases, when the boundary conditions do not prevent separation from spatial variables. Otherwise the problem may be solved approximately using numerical methods of which variations methods are mostly used. Unfortunately, the efficiency of variations methods declines in the case of mixed boundary conditions because of difficulties in building coordinate functions [1].
Therefore the development of approximate analytical methods for solving and analyzing these boundary value problems is a rather actual problem.
The problem of forced oscillations of thin homogeneous isotropic rectangular plate was considered. The plate 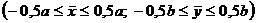 is hinged on
is hinged on 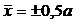 sides and on
sides and on 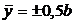 sides and has mixed boundary conditions of hinged-clamped type, symmetrical about the
sides and has mixed boundary conditions of hinged-clamped type, symmetrical about the  axis (Figure 1). Forcing pressure is applied to the plate:
axis (Figure 1). Forcing pressure is applied to the plate:
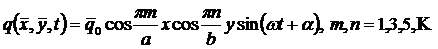
The differential equation for this problem is:
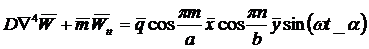 (1)
(1)
We will seek for its solution in the form of:
|
(2) |
After dimension removal and substitution of (2) to (1) we get:
|
(3) |
where 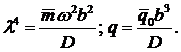
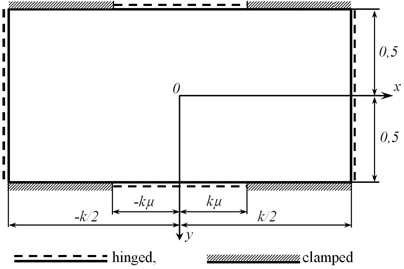
Figure 1. Plate with mixed boundary conditions
The 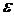 parameter is inserted into the boundary conditions in a way that provides fully hinged boundaries when
parameter is inserted into the boundary conditions in a way that provides fully hinged boundaries when 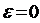 and considered boundary conditions when
and considered boundary conditions when  :
:
|
(4) |
|
(5) |
where 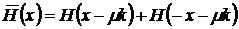 with
with 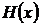 as Heaviside function.
as Heaviside function.
Presenting the form 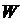 and eigenvalue
and eigenvalue 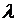 by
by 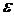 -based expansion (6) we can apply the pertrubation method to boundary value problem (3), (4), (5). [2]
-based expansion (6) we can apply the pertrubation method to boundary value problem (3), (4), (5). [2]
|
(6) |
A recurrent system of boundary value problems is obtained after asymptotic expansion of the original boundary value problem. Its solution is to be found in the form of:
|
(7) |
where 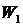 is a partial solution of non-homogeneous equation like (3) with homogeneous boundary conditions:
is a partial solution of non-homogeneous equation like (3) with homogeneous boundary conditions:
|
(8) |
while 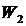 describes solution of the following boundary value problem:
describes solution of the following boundary value problem:
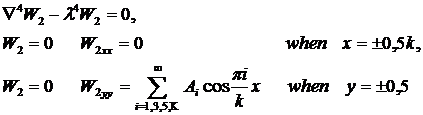
|
(9) |
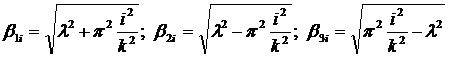 .
.
This system can be reduced to infinite system of algebraic equations and due to the necessity to satisfy boundary conditions (5), the next system is obtained:
|
(10) |
where

Presence of the 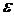 parameter in (10) allows us to simplify it by using the small parameter method and obtain recurrent formulas for determining the
parameter in (10) allows us to simplify it by using the small parameter method and obtain recurrent formulas for determining the 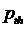 approximation of unknown coefficients:
approximation of unknown coefficients:
|
(11) |
|
(12) |
|
(13) |
The Pade approximation 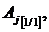 for which is: [3]
for which is: [3]
|
(14) |
Limits 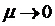 and
and 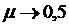 then give exact solutions for the (3), (4), (5) problem for corresponding
then give exact solutions for the (3), (4), (5) problem for corresponding 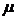 values.
values.
Plate forced oscillation problem for mixed boundary conditions of hinged-clamped type with non-symmetrical clamped area location can be solved analogically to the above shown method.
Considering the results obtained from the proposed method and numerical methods, the combination of boundary perturbation method and Pade approximation is applicable to plate forced oscillations problems with mixed boundary conditions of various types.
Literature:
1. Тимошенко С.П. Статические и динамические проблемы теории упругости / С.П. Тимошенко. – К.: Наук. думка, 1975. – 576 с.
2. Коул Д. Методы возмущений в прикладной математике / Д. Коул. – М.: Мир, 1972. – 227 с.
3. Бейкер Дж. Аппроксимации Паде / Дж. Бейкер, П. Грейвс–Моррис. – М.: Мир, 1986. – 502 с.