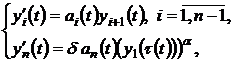Gorshkova P.G., Vareh N.V., Kostiv V.K.

Oles Honchar Dnipropetrovsk National University, Ukraine

RESEARCH OF DIFFERENTIAL MODELS WITH AFTEREFFECT WITH AN EVEN NUMBER OF EQUATION

Differential equations with delay of argument met in the works of Bernoulli in the eighteenth century, and then the results were used in the theory of sound. Further they are increasingly widely used in various fields of science, due to the fact that such equations are mathematical models of processes, change of speed which depends not only on their condition at this time, but also from the past (this is called the processes with aftereffect).

This work is devoted to the study of behavior solutions systems of the differential equations with deviating argument in the last equation with an odd number of equations in infinite and finite time interval (relatively to the second there is considered the system, which is a mathematical model of growth of population of the Earth on a finite interval of time). Let us consider a system of infinite time interval:

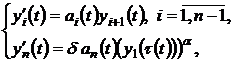(1)

Where: 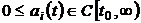, , 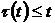,  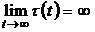– the ratio of odd numbers. The case 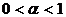 was investigated in the thesis work degree of the bachelor. The resultswere published in (1). Further research was conducted for linear and super linear case, namely  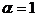and 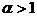.Here are the first obtained in theorems  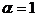n=5, .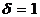

Theorem 1.

Let conditions be fulfilled:

1. α =1.

2.

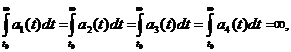
3.

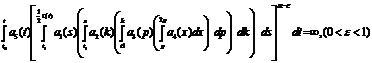
4.

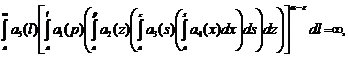
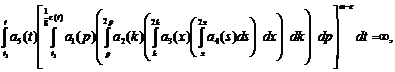
Then every solution of system (1) is either strongly oscillating, or each its component monotonically tends to infinity at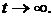 

At 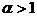, n=5,  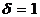there was obtained following

Theorem 2.

Let conditions be fulfilled:

1) a 

2) 

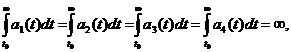
3) ,

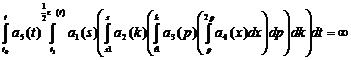4) .

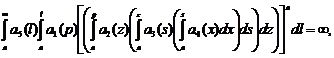5) 

Then every solution of system (1) is either strongly oscillating, or each its component monotonically tends to infinity at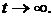 

Let us consider a system of differential equations with odd number of equations (n = 3), which is a mathematical model of growth of population of the Earth.To describe the demographic transition by Korotaev A.V., Malkova A.S, Dakhalturina D.A. there has been developed such a model:

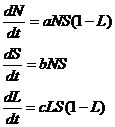
where N – the population number. S – a resource per capita of population, which can be spent on additional purposes – reproduction, science, art, entertainments and increase L-fate of literate population, a, b, c – constants. Impact of literacy on the demographic transition is expressed by the addition of factor (1 – L) and obtaining the equation. Let us create a new model, by the introduction of delay in to one of the equations:

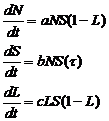
Where 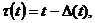 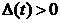 – delay. This, the introduction of delay we consider losses due to the influence of relative resource per capita of population in the past that affects the number of competent people, and this in turn to the population number at the present time. By lag input there is built more accurate model.

Literature:

1. Vareh N.V, Gorshkova P.G., Kykoyashna T.G., Marchenko A.V. «Research of Differential Eguations with Aftereffect», International Scientific Conference «Mathematical Problems of Technical Mechanics – 2011», Dnepropetrovsk-Dneprodzerzhinsk, p.61.