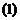
Hryhorzhevskaia A.Y., PhD Vareh N.V., Atanova M.Y.

Oles Honchar Dnipropetrovsk National University, Ukraine

STUDY ON DIFFERENTIAL AND FUNCTIONAL MODELS ON FINITE AND INFINITE INTERVALS

The state of many processes in the future depends not only on their state at present but also on the state in the past. The mathematical models of such processes are differential equations with the delay of argument [1].

This work is dedicated to the research of such systems. The conditions of strong oscillation of solutions on infinite time interval were received.

Let us consider the system

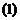
where , ,  ,  , .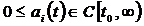

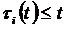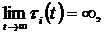
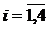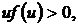
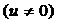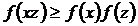The theorem was proven for the such system.

Theorem. Let the conditions be executed

1)  

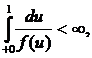
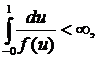
2)

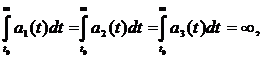
3) ,

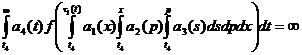4)

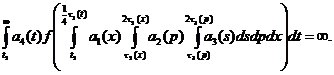
Then every solution 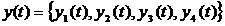 of the system (1) oscillates strongly.

A new economic and mathematical model that is based on the model of a small enterprise within the structure of an industrial complex was built on finite time interval. This model allows us to describe the co-operation and join development of small and big enterprises. The model also allows considering the influence of key production parameters and the degree of co-operation between small and big enterprises upon dynamics of small business enterprise development.

Thus the enterprise is described with using integrated characteristics: hypotheses of productivity of the enterprise, invariability and uniqueness of the applied technology etc. [3–4].

The development of small enterprise in Ukraine is accompanied by certain difficulties. These difficulties are caused that people who are involved in such activity, as a rule, have no economic and legal knowledge. It`s impossible to take any reasonable decision and make an effective strategy and tactics for the realization competitive activity with large companies without this knowledge. However a small enterprise has a possibility to join with a big enterprise [2]. Meanwhile a small enterprise aims at transforming from a competitor of a large enterprise in a partner of one.

There is a typical scheme of co-operation of a small and a big enterprise:

big enterprise, K

small enterprise, A

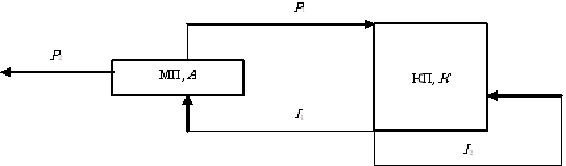
The scheme of co-operation small and large enterprises

The choice of the best form of co-operation of a small and a big enterprise implies the development of the mathematical model corresponding to the scheme.

Let us consider the system

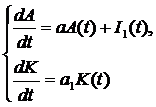 (2)

where , .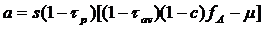

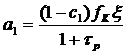The system of equations (2) determines an interconnected development of the small and the big enterprise. The stage of formation of the small enterprise was considered. On the initial steps of development a contribution of the small enterprise to the development of the general productive fund of the big enterprise is insignificant. Consequently the investments are also small too. It means that the big enterprise can choose four strategies of investing the small one:

1) permanent in time investments – ;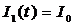

2) linear growing in time investments – ;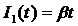

3) investments which are proportional to the general productive fund of the big enterprise – 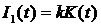, with permanent coefficient k;

4) investments which are proportional to the general productive fund of the big enterprise – 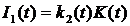, with coefficient .

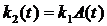Let us consider the economic sense of these schemes. Permanent in time investments have sense to be chosen in that case, when the development of the small enterprise requires approximately the same investment over the horizon planning (development period of the small enterprise). Linear growing in time investments can provide the significant growth of the general productive fund of the small enterprise on this time interval. Investments which are proportional to the general productive fund of the big enterprise with the permanent coefficient k reflect the ability of the big enterprise on investing the small one. Actually these investments are the permanent part of reinvestments of the big enterprise. The fourth scheme can be chosen when the basic task of investing of the big enterprise is speed-up development of the small enterprise.

A new model on the basis of the above mentioned model was constructed in this work. It takes into account the investment made in the past by a big enterprise in a small one.

The differential equations with delay of argument are reduced to normal equations without rejecting argument by classic method of steps [1]. The numerical method, namely the Runge-Kutte of the 4th order precision was applied to these equations.

Literature:

1. Elcgolc L. E. Introduction in the theory of the differential equations with a delay argument / Elcgolc L. E., Norkin S. B. – P.: Наука, 1971. – P. 12–58.

2. Hachatrian S. R. Models and methods of the solutions of economic problems/ Hachatrian S. R., Pinehina M. V., Buianov V. P. – P.: Экзамен, 2005. – P. 384.

3. Dilenko V. A. Economic and mathematical models of innovative activity of the industrial enterprise / Dilenko V. A., Shpak S. A. // Industrial economy. 2005. – №1. – P. 44–53.

4. Ehorova N. E. Application of the differential equations for the analysis of dynamics of progress of the small enterprises using a credit-investment resource / Ehorova N. E., Hachatrian S. R. // Economy and mathematical methods. – 2006. – №1. – P. 50–67.