Kotova Y.H., Kuzmenko V.I., Atanova M.Y.

Oles Honchar Dnipropetrovsk National University, Ukraine

MATHEMATICAL MODEL OF RECOVERY OF THE TEMPERATURE AREA WITH INCOMPLETE EXPERIMENTAL INFORMATION

If we know the dependence on time of the heat flow or the dependence on temperature on the border of the solid we will be able to determine the temperature distribution throughout the solid. This is the direct problem.

In many cases, the law of changing the heat flow or the surface temperature has to be determined by the measurements of the temperature in one or more interior points of the solid when we analyze dynamic processes. This is the inverse problem. The specific problem of estimating the term boundary condition on the results of measurements of the internal temperature is called the inverse problem of heat conduction. It is much more difficult to obtain an analytical solution of the inverse heat conduction problem than to find an analytical solution of the direct problem. It is much easier to carry out sufficiently accurate measurement of time dependences of temperature in interior points or at heat-insulated solid surface. Thus, we have to choose between relatively imprecise measurements and complex analytical task. At the same time the sufficiently accurate and easily realizable solution of the inverse problem would allow us to reduce both problems to a minimum simultaneously.

The problems of determining the laws of changing the temperature and the heat flow on the heated surface are equivalent in the sense that if one of these quantities is known then it could be quite easy to determine the other. It is impossible to determine them independently from each other because the only one boundary condition can be set at the moment at its boundary in the direct problem of the heat conduction. But that it is more difficult to calculate the heat flow accurately than the temperature of the surface.

We consider N points of measurement with the temperature in each T(P1), T(P2), …, T(PN). We have to find the temperature at all points of the solid so that the heat conduction equation carried out and the temperature in the points of measurement coincided with the least measured. We introduce n-point sources provided that n ≠ N. The source points create the temperature area. It satisfies Laplace equation:

 Δu = 0.    (1)

We use the fundamental solution of Laplace equation:

 .    (2)

We look for the solution:

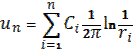. (3)

from the condition of minimum of the function of several variables:

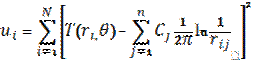.    (4)

The С1, С2, …, Сn values can be found from the system of linear algebraic equations. It was obtained by the required condition of extremum. We could find the solid temperature by the formula (3) after that. We study the convergence of the method when the number of points of measuring is increasing.

The inverse problem of heat conduction is one of the many ill-posed tasks in the mathematical sense. These problems are usually inverse and their solution is extremely sensitive to errors in the changes. There are several general methods for solving ill-posed problems. One of them is designed by Tikhonov. It is called the method of regulation and allows us to reduce the sensitivity of the solution to errors of measurement.

An incompact set V is considered, so there are minimizing sequences for extremal problem.

.   (5)

It is impossible to select subsequences which match with the solution of extremal problem from them in the selected metrics. The Tikhonov method is to replace an extreme problem for the functional J(ν) with the extreme problem for the another functional T(ν,α) on the set of Vα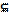V. Functional T(ν,α) must satisfy these conditions:

1) minimizing subsequence that occurs when we solve an extremal problem approximately

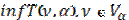,   (6)

converges to the solution of the original extremal problem;

1) the solution of extremal problem (6) converges to the initial solution of extreme problems.

So the idea of the method is to replace the incorrect extremal problem with the sequence of correct extremal problems. We often use so-called Tikhonovs’ functional during the implementation of this idea:

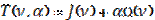. (7)

We perceive Ω(ν) as a functional which defined on the set VαV and takes only nonnegative values. A numeric parameter α≥0 is called the parameter of regulation. When α=0the functional T(ν,α) and J(ν) converge.

Literature:

1. Бек Дж. Некорректные обратные задачи теплопроводности: пер. с англ./ Дж. Бек, Б. Блакуэлл, Ч. Сент-Клэр, мл. – М.: Мир, 1989. – 312 с.

2. Кузьменко В.І. Конспект лекцій із курсу «Некоректні задачі» / В.І. Кузьменко. – Д.: РВВ ДНУ, 2009. – 76 с.