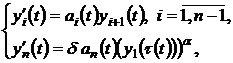Kukoyashna Т.G.,Vareh N.V., Kostiv V.K.

Oles Honchar Dnipropetrovsk National University, Ukraine

RESEARCH OF THE SYSTEMS WITH THE EVEN AMOUNT OF DIFFERENTIAL EQUATIONS WITH DEVIATING ARGUMENT AND NON-LINEARITY IN THE LAST EQUATION

Differential equations with deviating argument are widely used in various fields such as physics, biology, economics, mechanics, theory of automatic control. This is because these equations are mathematical models of processes, the rate of change of which depends not only on their condition at a given time (as for ordinary differential equations) but also from the past. These are so called processes with aftereffect.

This paper is devoted to the research of behavior of solutions of the systems of differential equations with deviating argument in the last equation with the even amount on the infinity interval, and research of system that is mathematical model in the medicine of distribution and control of tuberculosis, on the finite interval.

Consider system:

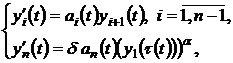(1)

where , , ,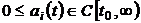

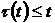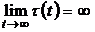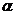 – relation of odd numbers.

In the paper [1] there have been presented results of research of solutions of the system (1) when 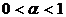, there also received results at 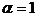. This paper we shall have given the results of research solutions of system when .

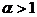Let us give one of the theorem when n=4, .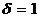

Theorem. If conditions have been satisfied:

1)  

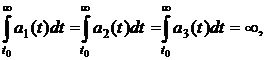
2) 

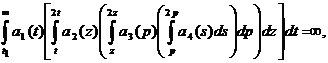
3)

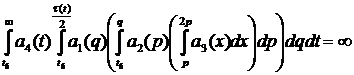
4)

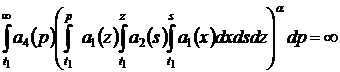
then every solution of system (1) is either strongly oscillatory, or each component of the solution tends monotonically to zero or to infinite as .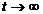

It is known, that order of system influences on character of solutions in general. If n is odd (n=5), 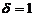, similar conditions ensure either strongly oscillatory of solutions, or tend monotonically to infinite, when  and if n is even (n=4) , every solution is strongly oscillatory.

Let us consider mathematical model of distribution and control of tuberculosis without deviating .

Modeling population is divided by sensitive (S), sick (Т), recently infected with high risk of disease deelopment 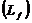 and a group of long-livin infectedg individuals who have low risk of disease development 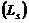. Person of group  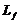and 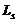 get chemioprophylaxic, the effect of which is described by rate constants 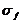and 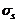 respectively. Solving system was carried out numerically by the method of Runge-Kutta.

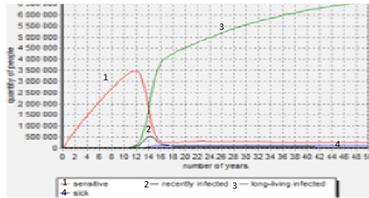
1. Mathematical model of distribution and control of tuberculosis without deviating

New model was built with entry of deviating argument. It considers that the person was treated in the past and moved to the vulnerable groups. Get:

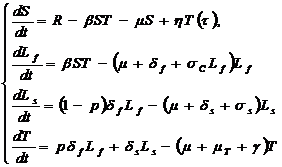
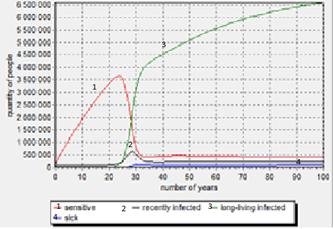
2. Model with entry of deviating argument

The chart has aproximately the same results as in previous models, they differ only by occurring in time. So, results of both these models are similar, it indicates that the viral disease of tuberculosis is sufficiently stable.

Literature:

1. Vareh N.V., Gorshkova P.G., Kukoyashna T.G.,Marchenko A.V. “Research of differential equations with aftereffect” , International Scientific Conference Mathematical problems of Technical Mechanics -2011”, Dnipropetrovsk-Dniprodzerzhinsk, p.61.