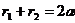Makhinya D.A., Vareh N.V., Kostiv V.K.

Oles Honchar Dnipropetrovsk National University, Ukraine

THE STUDY OF CURVES THE ELLIPSE AND THE HYPERBOLA

Definition of ellipse is the locus of points in the plane. For which the sum of the distances from two fixed points F1 and F2 of this plane, called foci, is the constant. This does not prevent the coincidence of the foci of the ellipse.

Obviously, if the foci coincide, then the ellipse is a circle. To derive the canonical equation of an ellipse about the beginning O we choose a Cartesian coordinate system in the middle of the segment F1F2, and the axes Ox and Oy are directed as shown in Figure 6.2 (if F1 and F2 foci coincide, then O coincides with F1 and F2, and for the axis Ox one can take any axis passing through O). Let the length of the segment F1 F2 be equal to 2c, then in the chosen system of coordinates F1 and F2, respectively, have coordinates (-c, 0) and (c, 0). Let us denote the constant by 2a referred to in the definition of an ellipse. Obviously,   2a> 2c, i.e., a> c. Let M-be the point of the plane with coordinates (x, y). Let r1 and r2 are the distance from point M to points F1and F2, respectively. According to the definition of the ellipse equation

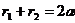.   (1)

Is a necessary and sufficient condition for the location of the point M (x, y) on this ellipse. Using the formula for the distance between two points, we obtain

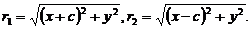.   (2)

From (1) and (2) ensues that the relation:

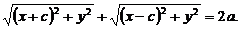(3)

It is a necessary and sufficient condition for the location of the point M with coordinates x and y on this ellipse. Hence the relation (3) can be considered as an equation of the ellipse. By taking the standard "radical destruction", this equation reduces to:

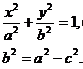 (5, 6)

Since the equation (4) is a consequence of an algebraic equation of the ellipse (3), then x and y coordinates of any point M of the ellipse will satisfy the equation (4). Since at the algebraic transformations related to getting rid of the radicals there could appear "excessive roots," we must make sure that any point M, whose coordinates satisfy the equation (4), is located on this ellipse. To do this, it is obviously sufficient to prove that r1 and r2 values for each point satisfy the relation (1). So, let x and y coordinates of the point M satisfy the equation (4). Substituting the value 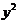 of (6.4) in the right-hand side of expression (2) for r1, after simple transformations, we find that: . Since 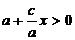, then 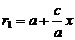. Quite similarly, we find that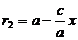. Thus, for a given point M:

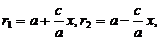 (6)

That is to say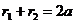, and, therefore, the point M is located on the ellipse. Equation (4) is called the canonical equation of an ellipse. The values of a and b are called, accordingly, the major and minor semi-axes of the ellipse.

Remark. If the semi-axis of the ellipse, a and b are equal, then the ellipse is a circle whose radius is R = a = b, and the center is the origin of coordinates.

Definition of a hyperbola is the locus of points in the plane, for which the absolute value of the difference between the distances to two fixed points F2 F1 of this plane, called foci, is the constant.

To derive the canonical equation of the hyperbola we choose the origin at the middle of the segment F1 F2, and the axes Ox and Oy are directed as shown in Figure. 6.2. Let the length of the segment F1 F2 = 2c. Then in this chosen coordinate system the points F1 and F2, respectively, have coordinates (-c, 0) and (c, 0). Let us by 2a denote the constant referred to in the definition of hyperbola. Obviously 2a <2c, i.e., a <c.

Let M be the point of the plane with coordinates (x, y) (Figure. 6.2). Let us denote by r1 and r2 the distances MF1 and MF2. According to the definition of a hyperbola, the equation:

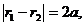(7)

Is a necessary and sufficient condition for the location of the point M on this hyperbola. Using expressions (2) for r1 and r2, and the relation (7), we obtain the following necessary and sufficient condition for the location of the point M with coordinates x and y at this hyperbola:

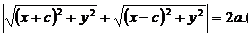 (8)

Using the standard method of "radical destruction", we reduce the equation (8) to the form:

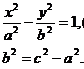(9, 10)

We need to make sure that the equation (9) is obtained by algebraic manipulations of equation (8), has not acquired new roots. It suffices to prove that for every point M, x and y coordinates of which satisfy the equation (9). The value r1 and r2 satisfy the relation (7). Using arguments similar to those that have been made in the derivation of formulae (6), we obtain for the quantities we are interested in r1 and r2 the following expressions:

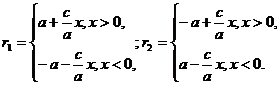  (11)

Thus, for a given point M, we have  and therefore it is located on the hyperbola [1].

Literature:

1. Ilyin, Analytical geometry.