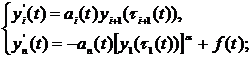
(1)
Marchenko A.V., Vareh N.V., Atanova M.Yu.
Oles Honchar Dnipropetrovsk National University, Ukraine
RESEARCH OF THE DIFFERENTIALLY-FUNCTIONAL MODELS AND SOME OF THEIR APPLICATIONS
This work is concerned with the behavior of solutions of differentially-functional systems such as differential equation system, which contains the retarded argument in the each equation and external influence in the last equation. The mentioned systems are the mathematical models, which are used for the description of effects and processes with aftereffect (the processes, which future condition is defined not only with the present condition, but also with the past condition) and some external influence.
Let us consider the following system:
|
(1) |
with the next assumptions: 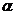 is the ratio of two odd natural numbers,
is the ratio of two odd natural numbers, 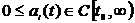 ,
,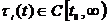 ,
,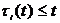 ,
,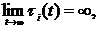 де
де 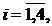
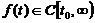 (2) [1].
(2) [1].
The behavior of the solution of the differential equation system (1), (2) was ascertained for 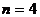 on the infinity in the case, when some external influence is absent, and in the case of existence of the external influence. Give below some certain theorems, which demonstrate the received results.
on the infinity in the case, when some external influence is absent, and in the case of existence of the external influence. Give below some certain theorems, which demonstrate the received results.
The conditions of strong oscillation of solution of differential equation system(1) with assumptions (2), where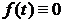 , in the case
, in the case 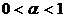 and
and 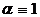 were obtained in works [1],[2]. Similar conditions for
were obtained in works [1],[2]. Similar conditions for 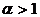 were found in this research.
were found in this research.
Theorem 1:
Let 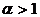 ,
, 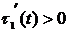 and next conditions are satisfied:
and next conditions are satisfied:
1) 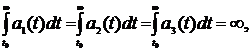
2) 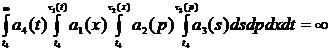 ,
,
3) 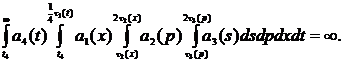
Then the each solution of the system (1) with assumptions (2) strongly oscillates.
Asymptotic behavior of system (1), (2) solution was previously ascertained in the work [2] for  in case, when some external influence is present (
in case, when some external influence is present ( ). But gained conditions don’t guarantee simply strong oscillation, they defend that solution of system (1)
). But gained conditions don’t guarantee simply strong oscillation, they defend that solution of system (1) 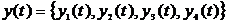 , which has the first component limited
, which has the first component limited 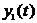 , strongly oscillates or
, strongly oscillates or 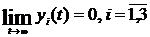 and
and 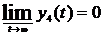 . Therefore it’s reasonable to search out the conditions, which will ensure only strong oscillation of solutions for
. Therefore it’s reasonable to search out the conditions, which will ensure only strong oscillation of solutions for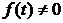 .
.
Theorem 2:
If the next conditions are fulfilled:
1) 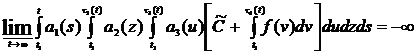 ,
,
2) 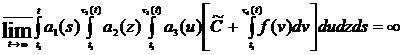 ,
,
3)  ,
, 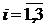 ,
,
then all solutions of system (1) with assumptions (2) oscillate.
This work is also devoted to the numerical research of differential equation system on the finite time interval. Lanchester’s mathematical model of war fighting was researched in this work. The following differential equation system describes the mentioned model:
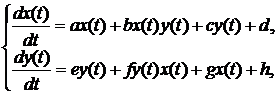
where a and e – speed of not combat losses; b and f – speed of losses from influence on area targets; c and g – losses from the influence of enemy troops in front; d and h– influence of the reserves.
The application domain of such models is very extensive: Lanchester’s model is used for the description of ethnic groups interaction, which live on common territory, as a model of competitive interaction of sales volume of two companies, for analysis of historical information.
In this work a new more generalized model was built. It includes deviating arguments. The obtained model is the following:
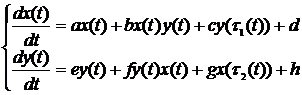 ,
,
where 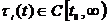 ,
, 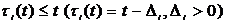 ,
, 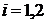 .
.
The mentioned model takes into account an essential impact of quantity of losses from influence of enemy troops in front, which occurred in the past, on the dynamic ofstrength of the each force, i.e. the future condition of strength of the each army depends not only on the present condition of losses, but also on the past condition.
Literature:
1. Варех Н.В. Дослідження диференціальних рівнянь з післядією / Н.В. Варех, П.Г. Горшкова, Т.Г. Кукояшна, А.В. Марченко // Міжнародна наукова конференція «Математичні проблеми технічної механіки – 2011». – Дніпропетровськ-Дніпродзержинськ. – С.61.
2. Марченко А.В. Дослідження диференціально-функціональних моделей та деякі їх застосування / А.В. Марченко, Н.В. Варех //Конференція за підсумками науково-дослідницької роботи ДНУ ім. О.Гончара «Проблеми прикладної математики та комп’ютерних наук». – Д.: ДНУ, 2011. – 41 с.