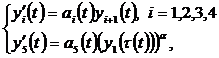Oliynik A.S., Varekh N.V., Atanova M.Y.

Oles Honchar Dnipropetrovsk National University, Ukraine

RESEARCH OF DIFFERENTIAL MODELS WITH ODD NUMBER OF EQUALIZATIONS WITH DEVIATING ARGUMENT OF MIXED TYPE

In this paper we investigate differential equations at infinite and finite time intervals.

The system with deviating argument is considered at infinite time interval

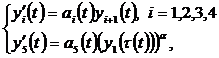(1)

where 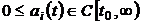,,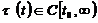 ,  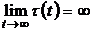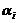– odd numbers relation.

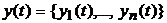 Let us consider the set of solutions  of system (1), which exist on  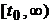and satisfies  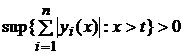at any .

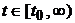Possibly, that functions which are included in the system (1) are such, that a set  is not empty.

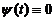
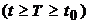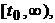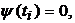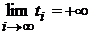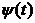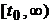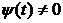Definition 1. A function   is called oscillating on  if there is an infinite set of values  of such, that  thus ; a function  is called no oscillating on , if  at .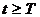

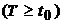Definition 2. The solution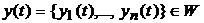 of the system (1) is called strongly (weakly) oscillating, if each (or at least one) of its component is an oscillating function.

 Definition 3. The solution 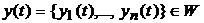 of the system (1) is called no oscillating, if each of its components is a no oscillating function.

 Let us give one of the received results.

The theorem was proved.

Theorem. Let the conditions be executed:

0<α<1 ,

, 

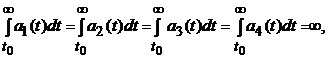
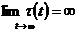
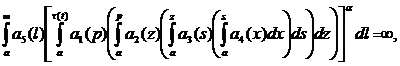
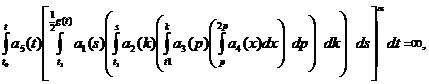
where g(t)=min 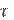{t,  (t)}.

Then every solution of the system (1) or oscillatory strongly, or each its component monotonically approaches to infinity at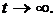 

A finite intervals Let us consider the dynamic model of industrial enterprise with participation of external investments, as the forms of state support on finite time intervals(S.R. Khachatryan’s model [1]) .

This model is adapted to the changes of external environment by the introduction the generalized function and the value a to the equation (2). They influence basic production assets. The dependences between the basic variable of enterprise model show the interconnection between aggregate variables. The mathematical model of this process is the following equation:

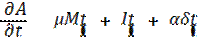(2)

  ,  ,  , ,

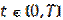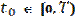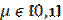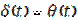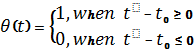
M(t)  – is a net income of an enterprise without tax deduction,

I(t) – are external investments,

a – is a value of external disturbance,

m  – a part of the net income, which is counted off on a reinvestment.

 Equation (2) describes the dynamics of capital stocks increase, at the expense of own resources and external investments. The influence of external factors with disturbance is taken into account here. The influence of disturbance takes place by introduction of generalized function.

 The model, in which the cost of capital stocks depends on the enterprise net income not only at this moment, but also on the past was built on the basis of this model by delay introduction. The second model, in which was taken into account, that the cost of capital stocks depends on both external investments at this moment, and the previous investments was also built.

Literature:

1. Герасимов Б.И. Дифференциальные динамические модели / Б.И. Герасимов, Н.П. Пучков, Д.Н. Протасов. – изд-во ГОУ ВПО ТГТУ, с.44.