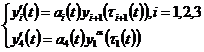Popova M.М., Sorokin V.І., Аtаnоvа М.Y.

Oles Honchar Dnipropetrovsk National University, Ukraine

RESEARCH OF DIFFERENTIAL MODELS WITH EVEN AMOUNT OF EQUATIONS WITH DEVIATION OF THE MIXED CHARACTER

This work deals with the research of the systems of differential equations with deviation of argument. Let us consider the system:

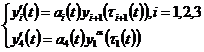   (1)

where 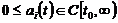, , 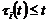 ,  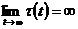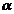– is relation of odd numbers.

The special case of the system (1) (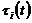≡ t, i=1,2,3  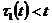) is considered in the work [1]. Unlike it in this work every equation includes deviation of argument. We’ll adduce one of the got results.

Theorem. Let the conditions be executed:

1) ,

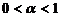2) ,

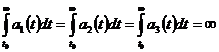
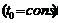3)

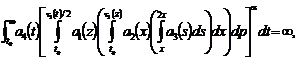
4),

5) 

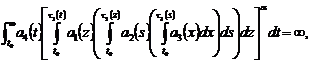
Then every decision of the system (1) either oscillates strongly, or each its component tends to zero or to endlessness at .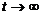

An analogical result can be got in the case, when deviation of argument is not only a delay, but it has the mixed character.

The formulated result relates to researches on an endless interval. Research of the differential systems is conducted also on a finite interval.

 The model of functioning of subsystem «a salesman and a buyer» is examined (networks of sale of fuel in the republic of Khakassia).

 The market of fuel is chosen as an object convenient for the application of the offered model.

 The daily changes of volumes of sales of petrol depend on different events: festive and output days, climatic and seasonal factor, volume of purchases, price and dynamics of processing of oil, psychological features of people behaviour, etnocultural state of society and others.

 We will consider a chain, included in a network structure and consisting of the consistently united elements «a salesman and an ultimate consumer», which can be described with the system (2) of usual differential equations of the first order with permanent coefficients through the functions of volume Q(t) and price p(t)

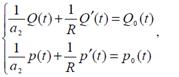  (2)

with starting conditions 

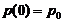
 For this chain realization of decision of the system (2) is shown on the basis of some statistical information.

 Coefficients are determined:

 1)  characterizing the speed of change of volume depending on the change of price;

 2) elasticity of supply at price;

 3) conductivities of goods on a chain.

 At the change of cost of salesman motion to the stable state is observed in the process of purchase-sale (Fig. 1), where the dotted line indicates actual information, continuous line shows model values. Values Q0 < Qy and Р0 < Рy, consequently, the functions of price and volume increase to the set values.

 The function of supply describes micromarket with the monopoly of salesman. At the examined market the function of р(t) will attain the value of py for the small interval of time. It testifies to practically unlimited possibilities of salesman, capable of quick taking of price to the set (desired) value.

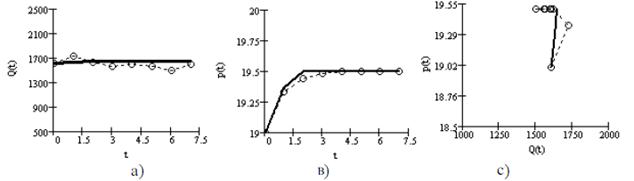
Fig.1. Change functions in time:

a) Price P(t); в) volume Q(t);  c) in the plane (Q(t), P(t))

 At the small conductivity of R (characteristic for firms, related to small business) and a2>>0, => Es>>0. The function of supply answers the conditions of existence of pure competition of salesman. On this micromarket a salesman requires much more time for taking of price to ру, as he is not able to influence on an ultimate consumer because of the small volumes of sale of goods.

 The mathematical model of dynamics of prices and volumes of sales is worked out, based on the theory of linear electric chains, theory of demand and supply, principles and methodology of economic physics.

 Stability of connection «a salesman and a buyer» is appraised on the basis of the got mathematical model, that allows exposing the scopes of functioning possibilities of market subjects.

 An economic model is being built and probed on the basis of this known economic model which takes into account aftereffect.

Literature:

1. Варех Н.В. Дослідження диференціальних рівнянь з післядією / Н.В. Варех, П.Г. Горшкова, Т.Г. Кукояшна, А.В. Марченко // Міжнародна наукова конференція «Математичні проблеми технічної механіки – 2011». – Дніпропетровськ-Дніпродзержинськ. – С.61.