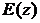 and Poisson ratio
and Poisson ratio 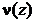 are the functions that change with the width of the strip. Normal and tangential load are applied to the top free border of the band. These loads operates within the finite area, or have the character of the periodic load.
are the functions that change with the width of the strip. Normal and tangential load are applied to the top free border of the band. These loads operates within the finite area, or have the character of the periodic load. Rakita O.Y., Lamzyuk V.D., Atanova M.Y.
Oles Honchar Dnipropetrovsk National University, Ukraine
PLANE DEFORMATION OF INHOMOGENEOUS BAND
We consider the elasticity theory plane problem for an inhomogeneous band, that is situated on an absolutely rigid foundation. Band is coupled with the foundation or has a smooth contact with it. The band inhomogeneity is concerned with the fact that the Jung 's modulus 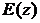 and Poisson ratio
and Poisson ratio 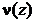 are the functions that change with the width of the strip. Normal and tangential load are applied to the top free border of the band. These loads operates within the finite area, or have the character of the periodic load.
are the functions that change with the width of the strip. Normal and tangential load are applied to the top free border of the band. These loads operates within the finite area, or have the character of the periodic load.
The pliancy functions method is used for solving this problem. Using Fourier integral transformation and Hooke's law we can show that the calculation of band stress-strain state is reduced to boundary problem solving for the usual differential equations system with variable coefficients in the Fourier transform space.
The method of reducing this boundary problem to two initial-value problems solving is processed. The first initial-value problem is the problem concerning pliancy functions. The second initial-value problem is the problem for differential equations system that was constructed earlier. We use the idea of pliancy functions to construct the full set of initial conditions. Pliancy functions depend on the structure of initial differential equations system and boundary conditions character, but not on their values. Thus, pliancy functions may be constructed before solving the concrete problem. It is significant that this method doesn’t require solving any of linear algebraic equation systems.
Pliancy functions calculation is also useful because it may be applied when contact problems are solved. We construct integral equations kernels by means of pliancy functions.
We conducted the research of pliancy functions properties. Pliancy functions behavior is determined when module of Fourier integral transformation parameter is increased.
The algorithm of calculating band stress-strain state is suggested. We examined the cases of concentrated force and dispersed normal load.
Software product for calculating pliancy functions and their asymptotic behavior was developed using Matlab 7 environment. We list pliancy functions calculations results for concrete the Jung 's modulus and Poisson ratio. Cases when Jung 's modulus is constant, increasing, decreasing function and a function with an optimum are described.
Cauchy problem concerning pliancy functions is the following
|
(1) |
|
(2) |
We determined, that if 
|
(3) |
Let’s view pliancy functions behavior for concrete parameters. Pliancy functions asymptotic behavior when 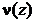 =0.3,
=0.3, 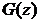 =const is displayed in Figure 1 and Table 1.
=const is displayed in Figure 1 and Table 1.
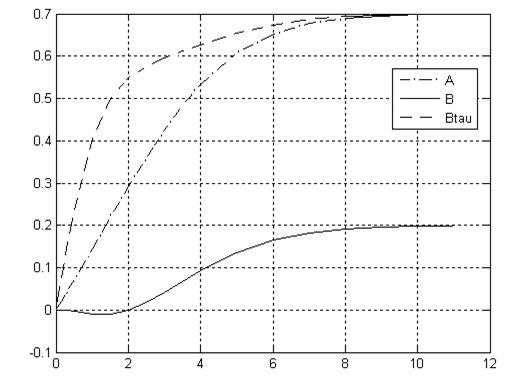
Fig. 1. 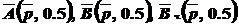
when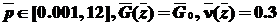
Table 1. Functions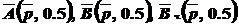 when
when 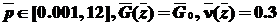
|
|
|
|
|
|
|
|
0.0010 |
0.0001 |
0.0000 |
0.0005 |
3.0000 |
0.4253 |
0.0410 |
0.5951 |
0.0100 |
0.0014 |
0.0000 |
0.0050 |
3.5000 |
0.4831 |
0.0668 |
0.6118 |
0.0200 |
0.0029 |
0.0000 |
0.0100 |
4.0000 |
0.5329 |
0.0923 |
0.6273 |
0.0500 |
0.0071 |
0.0000 |
0.0250 |
5.0000 |
0.6073 |
0.1357 |
0.6545 |
0.1000 |
0.0143 |
-0.0002 |
0.0499 |
6.0000 |
0.6523 |
0.1651 |
0.6742 |
0.2000 |
0.0286 |
-0.0007 |
0.0990 |
7.0000 |
0.6768 |
0.1823 |
0.6864 |
0.3000 |
0.0429 |
-0.0015 |
0.1467 |
8.0000 |
0.6892 |
0.1915 |
0.6933 |
0.5000 |
0.0717 |
-0.0039 |
0.2355 |
9.0000 |
0.6951 |
0.1960 |
0.6968 |
1.0000 |
0.1446 |
-0.0101 |
0.4040 |
10.0000 |
0.6978 |
0.1982 |
0.6985 |
1.5000 |
0.2183 |
-0.0101 |
0.4991 |
11.0000 |
0.6991 |
0.1992 |
0.6994 |
2.0000 |
0.2910 |
-0.0005 |
0.5481 |
12.0000 |
0.6995 |
0.1996 |
0.6997 |
Thus, we determined that pliancy functions calculated using the software product asymptotic behavior corresponds to with obtained theoretic estimations.