Международная студенческая научно-практическая конференция «Инновационное развитие государства: проблемы и перспективы глазам молодых ученых». Том 3
Saievych K.S., Lamzyuk V.D., Atanova M.Y.
Oles Honchar Dnipropetrovsk National University, Ukraine
THE INFLUENCE OF PERIODIC LOAD ON A HEAVY BAND EXFOLIATION
We consider incomplete contact of a heavy band with a multi-layer foundation under external squeezing load in [1]. In this work the effect of periodic load on the nature of the contact zone between heavy band and multi-layer foundation under plane deformation is evaluated.
Let the heavy band of thickness h lay freely on the multilayer foundation. The material of the band is assumed to be homogeneous and isotropic. E, ν and ρ-respectivelyYoung's modulus, Poisson ratio and relative density of the material strip. Vector volume force is directed vertically downward and equals gρ, where g – acceleration of free fall.
Further, we take the package of endless smooth or elastic bands linked that throughout the length adjacent to the half-plane (elastic or completely solid) as the multi-layeredbasis.
Modulus of elasticity ( ) and thickness
) and thickness 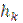 steel are within the each band, but during the transition from one band to another they can change by any law. The number ofbands in the base is assumed to be finite (n ≥ 1). Half-plane will be called the lower band number n. During the plane strain the strips of foundation are not behind each other.
steel are within the each band, but during the transition from one band to another they can change by any law. The number ofbands in the base is assumed to be finite (n ≥ 1). Half-plane will be called the lower band number n. During the plane strain the strips of foundation are not behind each other.
Let the upper limit of elastic bands be applied by external normal load (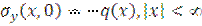 ), that presses the strip to the base, and tangential load (
), that presses the strip to the base, and tangential load (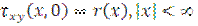 ).
).
Function q (x)-pair, r (x)-odd. And
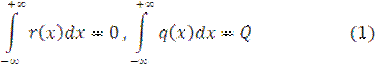
Before studying the contact problem of the backlog of heavy bands from multilayer base, we find out under what conditions the backlog of heavy bands from the base ispossible. To do this, we assume that there is no backlog between the heavy bar and the n – layer base. In this case the formula for calculation of contact stresses on the borderstrip and n-layer base has the form

Where 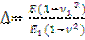 ,
, 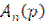 - compliance function [2], x and y-abscissa and ordinate respectively in Cartesian coordinate system (see Fig. 1).
- compliance function [2], x and y-abscissa and ordinate respectively in Cartesian coordinate system (see Fig. 1).
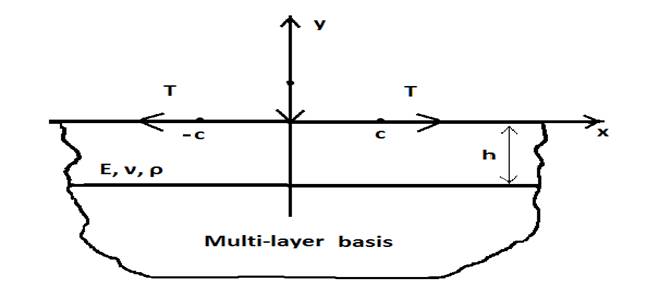
Fig. 1
The equation (2) makes it possible to establish the conditions under which in some areas outside the contact zone and heavy foundations are positive normal load 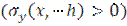 , that is, under what conditions a heavy band is behind the base.
, that is, under what conditions a heavy band is behind the base.
It was found that not for any normal q (x) and tangent r (x) load distributed in the area of finite length of the upper limit of the heavy band, band gap from the base is possible.A similar conclusion is in work [1], where  .
.
For example, let a heavy band touch (Fig. 1) the elastic half-plane (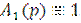 ) with the concentrated force
) with the concentrated force 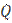 (
( ) and the upper limit of the band has the same balance in their tangential stress
) and the upper limit of the band has the same balance in their tangential stress 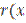 )=
)=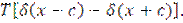 Then if the full contact with the base of heavy bands exists, normal tension on the border strip and half-plane is calculated by the formula
Then if the full contact with the base of heavy bands exists, normal tension on the border strip and half-plane is calculated by the formula
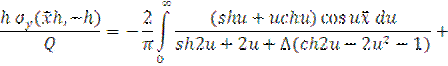
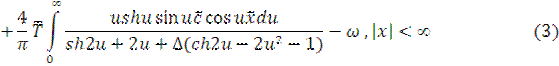
де

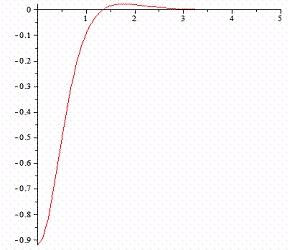
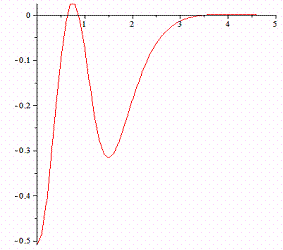
To calculate the integrals in (3) we used the method FILON [3] and the asymptotic formula. The results of calculations (Fig. 2) allow us to conclude under which conditions (parameters 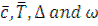 ) behind the heavy band and the elastic half-plane backlogs are possible. Also the influence of parameters
) behind the heavy band and the elastic half-plane backlogs are possible. Also the influence of parameters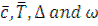 on the number of possible areas of contact of the heavy band with the base band was found.
on the number of possible areas of contact of the heavy band with the base band was found.
 +ω
+ω 
 +ω
+ω 

Literature:
1. Ламзюк В.Д. О неполном контакте тяжелой полосы с основание / В.Д. Ламзюк // Вопросы прочности и пластичности. – ДГУ, 1993.-С.58-68.
2. Приварников А.К. Пространственная деформация многослойного основания / А.К. Приварников // Устойчивость и прочность элементов конструкций. – Днепропетровск: ДГУ, 1973. – С. 78-100.
3. Крылов В.И. Приближенное вычисление интегралов / В.И. Крылов. – Н.: Наука, 1967.
 ) and thickness
) and thickness 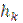 steel are within the each band, but during the transition from one band to another they can change by any law. The number ofbands in the base is assumed to be finite (n ≥ 1). Half-plane will be called the lower band number n. During the plane strain the strips of foundation are not behind each other.
steel are within the each band, but during the transition from one band to another they can change by any law. The number ofbands in the base is assumed to be finite (n ≥ 1). Half-plane will be called the lower band number n. During the plane strain the strips of foundation are not behind each other.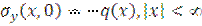 ), that presses the strip to the base, and tangential load (
), that presses the strip to the base, and tangential load (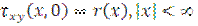 ).
). 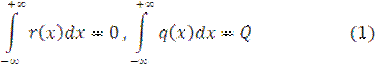

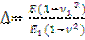 ,
, 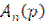 - compliance function [2], x and y-abscissa and ordinate respectively in Cartesian coordinate system (see Fig. 1).
- compliance function [2], x and y-abscissa and ordinate respectively in Cartesian coordinate system (see Fig. 1).
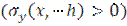 , that is, under what conditions a heavy band is behind the base.
, that is, under what conditions a heavy band is behind the base.  .
.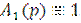 ) with the concentrated force
) with the concentrated force 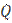 (
( ) and the upper limit of the band has the same balance in their tangential stress
) and the upper limit of the band has the same balance in their tangential stress 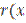 )=
)=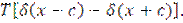 Then if the full contact with the base of heavy bands exists, normal tension on the border strip and half-plane is calculated by the formula
Then if the full contact with the base of heavy bands exists, normal tension on the border strip and half-plane is calculated by the formula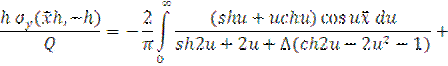
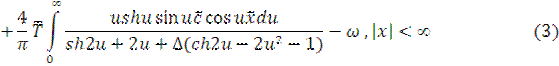

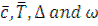 ) behind the heavy band and the elastic half-plane backlogs are possible. Also the influence of parameters
) behind the heavy band and the elastic half-plane backlogs are possible. Also the influence of parameters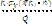 +ω
+ω 


