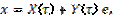
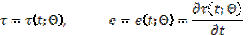 (1)
(1)Vazeh N.V., Belozerov A.V., Atanova M.Yu.
Oles Honchar Dnipropetrovsk National University, Ukraine
A NON-LINEAR SYSTEM USING A NON-SMOOTH TEMPORAL TRANSFORMATION
Solutions of differential equations of motion for mechanical systems with periodic impulsive excitation are represented in a special form which contains a standard pair of non-smooth periodic functions and possesses the structure of an algebra without division. This form is also suitable in the case of excitation with a periodic series of discontinuities of the first kind. All transformations are illustrated on the Duffing oscillator under a parametric non-equidistant pulsed forcing with a dipole-like shift of the impulses, although the technique can be applied to more general cases. An explicit form of analytical solutions has been obtained for periodic regimes. These solutions and numerical simulations indicate a principal role of the impulses' shift. Namely, the system performs periodic, multiperiodic and stochastic-like dynamical regimes if varying a parameter of the shift. The analytical approach is based on the limit of linear system under equidistant distribution of the impulses and asymptotically takes into account the dipole-like shift and non-linearity.
The representation is based on a proposition that an arbitrary periodic function x(t) (the period of which is normalized to four) can be expressed as
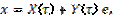
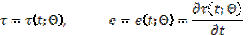 (1)
(1)
wheret is the saw-tooth piecewise-linear function of argument t and period equal to four; 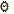 (-1<
(-1<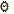 <1) is a parameter characterizing the slope of the "saw". Note that the period has been normalized to four, not to 2
<1) is a parameter characterizing the slope of the "saw". Note that the period has been normalized to four, not to 2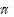 . A convenience of this choice is going to be discussed later. The second one consists of the Dirac functions
. A convenience of this choice is going to be discussed later. The second one consists of the Dirac functions 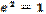 .
.
A FORMULATION OF THE PROBLEM
In order to illustrate the transformations consider the Duffiing oscillator under a parametric pulsed excitation. Define a coordinate of the system x=x(t),which is described by the following differential equation of motion
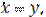 (2)
(2)
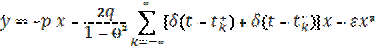
Where 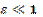 is a small parameter; the dot denotes differentiation with respect to time, t;p and q are constant parameters. The parametric pulsed excitation is expressed by means of the generalized second derivative of a saw-tooth piecewise-linear function
is a small parameter; the dot denotes differentiation with respect to time, t;p and q are constant parameters. The parametric pulsed excitation is expressed by means of the generalized second derivative of a saw-tooth piecewise-linear function 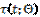 of argument tand period equal to four.
of argument tand period equal to four. 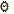 is a parameter characterizing the slope of the "saw".
is a parameter characterizing the slope of the "saw".
THE NON-SMOOTH TRANSFORMATION OF THE SYSTEM
It was mentioned above, that system (2) will be transformed first in order to eliminate the singular Dirac's functions. The case in point is the non-smooth temporal transformation in a manifold of periodic regimes. To provide this transformation, a periodic solution with the period T=4 is represented due to (1) by the following expression [1-3].
Note that the derivative 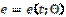 is a piecewise constant function. Hence, it can be verified that e2 =
is a piecewise constant function. Hence, it can be verified that e2 = 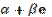 , where
, where 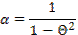 and
and 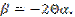
In the symmetric case (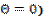 the relation reduces to equation
the relation reduces to equation 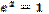 .
.
Another relation which will be taken into account is
 (3)
(3)
The first formal derivative is
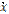 =
=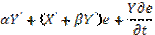 (4)
(4)
Substituting (1) into (2) and taking into account (3) and (4) gives
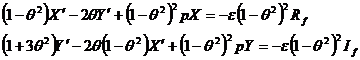 (5)
(5)
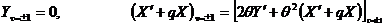 (6)
(6)
The related periodic solutions are
Ао = ±С0 = А, (7)
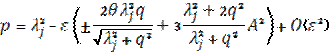
Expression (7) indicates a branching of curves p=p(q) on a plane of the system parameters, pq, when a non-zerothslope (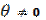 ) of the saw-tooth function appears. The branching generate instability regions on the parameters plane and strongly affects on the system dynamics.
) of the saw-tooth function appears. The branching generate instability regions on the parameters plane and strongly affects on the system dynamics.
CONCLUSIONS
In this paper the non-smooth temporal transformation has been applied to construct a family of periodic solutions of a weakly non-linear system under the parametric impulsive excitation. The transformation eliminates singular terms and reduces in the equation of motion to a standard weakly non-linear boundary value problem. To solve this problem asymptotic expansions were applied. As a result explicit form analytical solutions in terms of elementary functions have been obtained for small asymmetry of the distribution of impulses' sequences, (the dipole-like shift of each two neighboring impulses). The solutions and numerical simulations show a principal role of the shifts of the impulses' sequences.
Literature:
1. Pilipchuk V. N. Temporal transrmations and visualization diagrams for non smooth periodic motions // International Journal of Bifurcation and Chaos, Vol.15, No.6 . – 2005.
2. Pilipchuk V. N. A Non-Linear system using a non-smooth temporal transformation // Journal of Sound and Vibration. – 1999. -307-327.
3. Pilipchuk V. N. Non-smooth time decomposition for non linear models Driven by random impulses // Chaos, Solitons and fractals 14 2004 129-143