Azarevich A.O., Lamzyuk V.D., Atanova M.Y.
Oles Honchar Dnipropetrovsk National University, Ukraine
ABOUT EXFOLIATION OF MULTILAYER FOUNDATION IN VIEW OF TANGENT LOAD
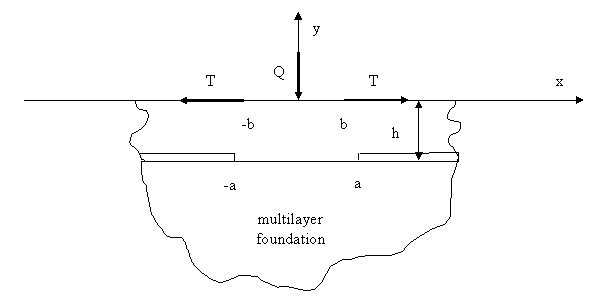
The planar problem of elasticity theory about partial contact of a smooth band with multi-layered foundation under the action of squeezing and tangent load was considered Figure 1. The material of band is assumed to be homogeneous and isotropic. Tangential load is required to be self-balanced for static equilibrium of the system (band-base).
Figure 1. Partial contact of a smooth band with multi-layered foundation
At first it is assumed that elastic band has a smooth contact with the entire surface of the multilayer foundation. The assumption about the impossibility of the lag of layers in the foundation is not always true [1]. A formula for determination of the normal contact tension on the border of the band and the foundation (1) was obtained with the use of previously developed method of compliance functions [2].
The same analysis of formula (1) as without tangent load allows us to conclude that unlimited zones of stretching contact tension appear in the case of finite normal load excluding the weight of the bands, that is smooth elastic band must lag behind the foundation.
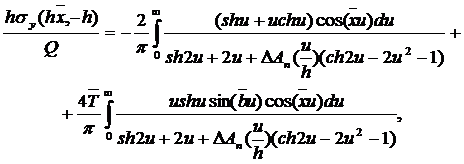
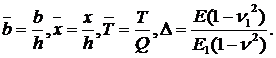
The number of possible areas of contact of the band with the foundation was analyzed. Table 1 shows the number of the contact areas when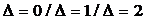
. The calculated experiments make it possible to assert that the change of parameters significantly effects on this process.
Table 1. The number of the contact areas when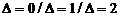
|
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1 |
1.25 |
1.5 |
1.75 |
2 |
5.4 |
2/2/1 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
3/3/2 |
3/3/2 |
3/3/2 |
3 |
1 |
2/2/1 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
3/2/2 |
3 |
3 |
3 |
2 |
1 |
1 |
2/1/1 |
2 |
2 |
2 |
2 |
2 |
2 |
3 |
3 |
3 |
3 |
3 |
1.77 |
1 |
1 |
2/1/1 |
2/2/1 |
2/2/1 |
2/2/1 |
2/2/1 |
2/2/1 |
3 |
3 |
3 |
3 |
3 |
3 |
1.6 |
1 |
1 |
1 |
2/1/1 |
2/1/1 |
2/1/1 |
2/1/1 |
3/3/1 |
3/3/1 |
3/3/1 |
3 |
3 |
3 |
3 |
1.4 |
1 |
1 |
1 |
1 |
1 |
1 |
3/1/1 |
3/1/1 |
3/1/1 |
3/3/1 |
3 |
3 |
3 |
3 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
3/1/1 |
3 |
3 |
3 |
3 |
0.633 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
3/1/1 |
3/3/1 |
3/3/1 |
3 |
0.3555 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
3/1/1 |
3/1/1 |
3/3/1 |
3/3/1 |
0.166 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
3/1 |
3/1/1 |
3/3/1 |
The technique for finding the real areas of contact of an elastic band with smooth layered foundation and distribution of contact pressure on these areas was offered. Singular integral equation with respect to contact pressure was built. It was established that a method which is described in [3] should be used for determination of the previously unknown boundaries of contact areas. A singular integral equation of the contact problem was regularized by Carleman-Vekua method.
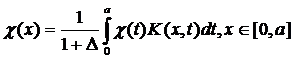
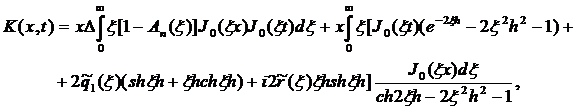
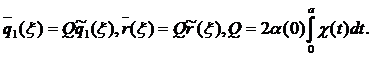(3)
A method of the mechanical quadrature was used for the numeric solution of the obtained Fredholm integral equation of the second kind (2), where the kernel has the form (3). As a result solving of the integral equation (2) was reduced to a homogeneous system of linear algebraic equations. Previously unknown boundary a of the contact area was found from the condition of the existence of nontrivial solution of this system. After the solution of the integral equation (2) the tension was calculated (4) on the contact area of the band with the foundation.
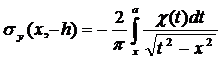.(4)
Solution (contact pressure) was found in the class of functions that are limited (equal zero) on the ends of the contact areas. The problem of incomplete contact of the smooth band with the foundation under concentrated normal load and the two tangent self-balanced forces was solved numerically.
Literature:
1. Lamzyuk V.D., Privarnikov A.K. The action of the stamp on a layer that can lag behind the foundation //Questions of strength and plasticity. – D.: DSU, 1971. – P. 58-77.
2. Privarnikov A.K. Spatial deformation of the multilayer foundation //Stability and strength of construction elements. – D.: DSU, 1973. – P. 27-45.
3. Lamzyuk V.D., Privarnikov A.K. Plane prolem about incomplete contact of the band with foundation //Questions of strength and plasticity. – D.: DSU, 1971. – P. 78-100.
