Международная студенческая научно-практическая конференция «Инновационное развитие государства: проблемы и перспективы глазам молодых ученых». Том 3
Baboshkin I.I., Kuzmenko V.І., Аtаnоvа М.Y.
Oles Honchar Dnipropetrovsk National University, Ukraine
RESEARCH OF MASSIVE STRUCTURES’ INFLUENCE ON HETEROGENEOUS BASES
Introduction
The necessity of making accurate estimations of buildings’ interaction with foundations arises in connection with intensification of building and regular building areas deficit. Nowadays building must be carried out on heterogeneous bases. That is why it is very important to carry out a research of non-uniform settlings which appears as the result of bases’ heterogeneity.
The main aim of this paper is to develop the models of non-uniform settlings of massive stamps to get deflected mode of bases using the contact problems theory for elastic solid.
1. Formulation of the problem
Plane deformation of heterogeneous band is being researched. The properties of the band are described by Lamé parameters 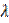 and
and 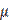 in each point of the band. The band is being deformed under the influence of the massive stamp with a flat foundation. As a result of the band deformation the stamp receives vertical shift (settling)
in each point of the band. The band is being deformed under the influence of the massive stamp with a flat foundation. As a result of the band deformation the stamp receives vertical shift (settling) 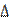 and rotation
and rotation 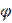 , that are considered to be given (Fig. 1).
, that are considered to be given (Fig. 1).
Let 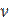 be the unit vector of outer normal to the band surface. Let the surfaces of the band and stamp be coupled. For further let
be the unit vector of outer normal to the band surface. Let the surfaces of the band and stamp be coupled. For further let 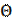 be dilatational strain:
be dilatational strain:
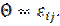
Therefore the problem lies in finding components of displacement vector 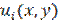 , small deformation tensor
, small deformation tensor  and stress tensor
and stress tensor 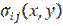 .
.
Mentioned characteristics have to satisfy equations of equilibrium

Cauchy relations

determinative relations

Moreover, conditions

must be satisfied on contact area of the stamp and the band.
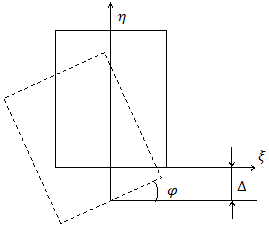
Fig. 1. Rotation and shift of the stamp
1. Variational problem formulation
Specified problem formulation is unsuitable for construction of numerical methods solution. The most natural is its variational formulation. Variational method allows us to use developed methods of discretization. The typical method of variational problem formulation is considered in [1].
In order to make a variational problem formulation we are going to introduce the set of allowable functions 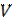 . In this set we will include all allowable displacement vectors
. In this set we will include all allowable displacement vectors 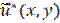 , which components are continuous functions and they have continuous partial derivatives and satisfy condition (4) on contact area with the band.
, which components are continuous functions and they have continuous partial derivatives and satisfy condition (4) on contact area with the band.
For the specified problem we have received extremal variational problem
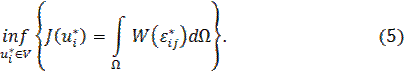
It means that we must find a valid displacement among all of the motions 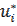 from the allowable set
from the allowable set 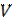 for which the minimal value of the functional
for which the minimal value of the functional
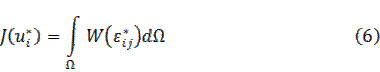
corresponds to.
2. Discretization of the received problem
For discretization of the problem we use finite element method (FEM) that is the most widely-spread at the moment. The characteristic zones of the band for building finite-element mesh are shown on the Figure 2. As the finite elements we will take rectangular FE with bilinear approximation of allowable function. Motions are linearly distributed on the boundaries of the finite element so it provides continuity of the motions on its boundaries.
After the substitution of expressions for displacement into the functional (6) we will receive a multivariable function 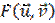 . We have received a problem of unconstrained optimization of the multivariable function. We will get a linear system of equations by using the necessary condition of extremum
. We have received a problem of unconstrained optimization of the multivariable function. We will get a linear system of equations by using the necessary condition of extremum
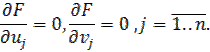
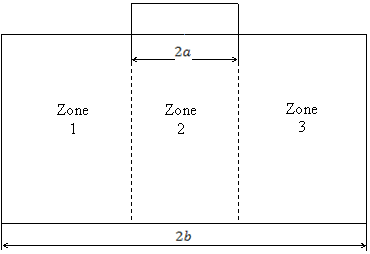
Fig. 2. Characteristic zones of the band for building finite-element mesh
3. Method of solution of received linear system
The matrix of the linear system that we would receive using FEM is very discharged. Iterative methods are very effective for such systems. The method of successive over-relaxation (SOR) is one of the most efficient numerical methods. This method is a variant of the Gauss–Seidel method and it allows us to substantially increase the speed of convergence of the iterative process. The detailed description of the SOR method is given in [2].
It is proven that for systems with positive-definite symmetrical matrix relaxation parameter  leads to convergence of iterative process. When
leads to convergence of iterative process. When 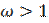 the method is called method of upper relaxation. The speed of iterative process convergence can be changed by choosing relaxation parameter value. That is why we can say about the optimal value of the relaxation parameter. It is known that there is optimal value
the method is called method of upper relaxation. The speed of iterative process convergence can be changed by choosing relaxation parameter value. That is why we can say about the optimal value of the relaxation parameter. It is known that there is optimal value 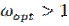 of the relaxation parameter for systems that have been received within method of SOR. In practice values of
of the relaxation parameter for systems that have been received within method of SOR. In practice values of 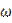 near the optimal
near the optimal 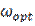 are being searched within computing experiment.
are being searched within computing experiment.
As a stopping criterion of the iterative process can be taken
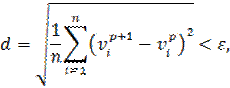
where 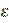 is a given constant that is called error parameter.
is a given constant that is called error parameter.
4. Received results
The specified problem was solved within the software that was created. It was found out that for this class of problems the optimal value of relaxation parameter can be taken as 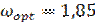 . The practical convergence of approximated solutions was shown.
. The practical convergence of approximated solutions was shown.
Literature:
1. Кузьменко В.И. Решение на ЭВМ задач пластического деформирования: справочник / В.И.Кузьменко, В.Ф.Балакин. – К.: Тэхника. – 136 с.
2. Кузьменко В.І. Вступ до методів скінченних елементів: навч. посіб. / В.І. Кузьменко. – Д.: РВВ ДНУ, 2002. – 84 с.
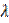 and
and 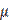 in each point of the band. The band is being deformed under the influence of the massive stamp with a flat foundation. As a result of the band deformation the stamp receives vertical shift (settling)
in each point of the band. The band is being deformed under the influence of the massive stamp with a flat foundation. As a result of the band deformation the stamp receives vertical shift (settling) 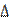 and rotation
and rotation 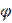 , that are considered to be given (Fig. 1).
, that are considered to be given (Fig. 1).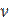 be the unit vector of outer normal to the band surface. Let the surfaces of the band and stamp be coupled. For further let
be the unit vector of outer normal to the band surface. Let the surfaces of the band and stamp be coupled. For further let 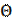 be dilatational strain:
be dilatational strain: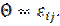
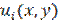 , small deformation tensor
, small deformation tensor  and stress tensor
and stress tensor 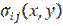 .
.




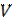 . In this set we will include all allowable displacement vectors
. In this set we will include all allowable displacement vectors 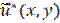 , which components are continuous functions and they have continuous partial derivatives and satisfy condition (4) on contact area with the band.
, which components are continuous functions and they have continuous partial derivatives and satisfy condition (4) on contact area with the band.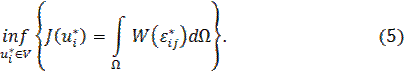
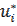 from the allowable set
from the allowable set 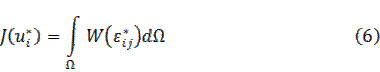
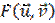 . We have received a problem of unconstrained optimization of the multivariable function. We will get a linear system of equations by using the necessary condition of extremum
. We have received a problem of unconstrained optimization of the multivariable function. We will get a linear system of equations by using the necessary condition of extremum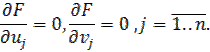

 leads to convergence of iterative process. When
leads to convergence of iterative process. When 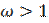 the method is called method of upper relaxation. The speed of iterative process convergence can be changed by choosing relaxation parameter value. That is why we can say about the optimal value of the relaxation parameter. It is known that there is optimal value
the method is called method of upper relaxation. The speed of iterative process convergence can be changed by choosing relaxation parameter value. That is why we can say about the optimal value of the relaxation parameter. It is known that there is optimal value 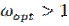 of the relaxation parameter for systems that have been received within method of SOR. In practice values of
of the relaxation parameter for systems that have been received within method of SOR. In practice values of 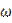 near the optimal
near the optimal 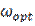 are being searched within computing experiment.
are being searched within computing experiment.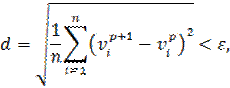
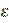 is a given constant that is called error parameter.
is a given constant that is called error parameter.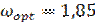 . The practical convergence of approximated solutions was shown.
. The practical convergence of approximated solutions was shown.