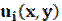 , small deformation tensor
, small deformation tensor 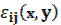 and stress tensor
and stress tensor 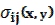 . Mentioned characteristics have to satisfy equations of equilibrium, Cauchy relations and determinative relations.
. Mentioned characteristics have to satisfy equations of equilibrium, Cauchy relations and determinative relations.Kirichenko A. N., Kuzmenko V. І., Аtаnоvа М. Y.
Oles Honchar Dnipropetrovsk National University
THERMOPLASTIC CONTACT PROBLEM OF CONNECTION LAYERS IN COMPOSITES
With the development of major industries it is necessary to use materials which have higher service properties. The best solution to this problem is to use the layered composite materials (CM), which incorporate not only the properties of the components, but are usually characterized by a range of new, often unique, qualities. So the research of CM behavior in real conditions is of primary importance.
Receiving valid results about deformation CM creates the preconditions to develop recommendations that allow us to minimize the undesirable effects. Such studies will help to assess the possibility of using CM and develop relevant recommendations.
Plane deformation of layered composite, which properties are described by Lame parameters λ and μ, is investigated. Deformation of the composite occurs under the action of plates with flat base. As a result of composite deformation plates receive vertical shifts (sags), which are considered to be given.
The problem is to find components of displacement vector 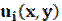 , small deformation tensor
, small deformation tensor 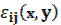 and stress tensor
and stress tensor 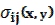 . Mentioned characteristics have to satisfy equations of equilibrium, Cauchy relations and determinative relations.
. Mentioned characteristics have to satisfy equations of equilibrium, Cauchy relations and determinative relations.
So, we must find the above functions, which satisfy the system (1)
|
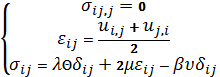
and boundary conditions
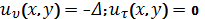 , for the upper border,
, for the upper border,
 , for the lower border,
, for the lower border,
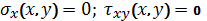 , on the sides.
, on the sides.
Formulated problem statement is not really usable for the construction of numerical methods of solution. The most natural is the variation formulation. The typical method of variation formulations construction of boundary value problems of elastic body theory is considered in [1]. A finite-element method was used for discretization of the problem. To approximate permissible functions the rectangular finite-elements were used.
Having substituted the expressions for the components of the vector displacement in functional of the extreme variation problem, we obtain a function of many variables. We received a problem of absolute minimization of quadratic functions of several variables. Let us write down the necessary condition for extreme. We receive a linear system of equations that was solved using method of successive over-relaxation (SOR).
Formulated problem was solved using the developed software.
The list of references:
1. Кузьменко В. И. Решение на ЭВМ задач пластического деформирования: Справочник / В. И. Кузьменко, В. Ф. Балакин. – К.: Тэхника. – 136 с.