Kochubey O. O., Yevdokymov D. V., Kriachunenko O. L., Deriy V. S.
Oles Honchar Dnipropetrovsk National University
MATHEMATICAL AND NUMERICAL MODELING OF MASS TRANSFER IN SOIL
Last years due to food crisis further development of agricultural industry has become one of the most important aim of Humanity. Development of agricultural industry is impossible without correspondent development of agricultural science. For example, a progress in plant-growing completely depends on success in agricultural science, but the last is connected with understanding of biological, chemical, mechanical and thermal processes in soils. Biological and chemical processes are investigated intensively using all opportunities of modern science. As for filtration flows and mass transfer processes in soils, which must be investigated mainly by mathematical tools, the unnecessary simplified mathematical models are used in this field. For example, roots of plants suck up water, that stimulates a specific filtration flows. However, cross-section area of plant root is negligibly small in comparison with reference size of whole domain. As a result, multiscale problems must be formulated as correct mathematical models of filtration in soils. In fact, multiscale problems have never used for this aim because of mathematical and computational difficulties are intrinsic to them. The similar situation takes place with sorption of salts dissolved in water by particle of rigid frame of soils, that was not considered properly. It is evident, that to improve the situation, new generalized mathematical models and algorithms of numerical solution must be proposed. The present work is to be considered as an attempt to provide some progress in this direction.
Generally speaking, there are two mathematical models of mass transfer in soil filtration model applied for water motion in saturated soil, and diffusive model by A.V. Lykov for unsaturated media. Accuracy and applicability of the second model requires additional special investigations and discussions. For the sake of simplicity, the following consideration will be restricted by the filtration model in plane case.
Let us consider a domain 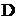 of saturated porous media. Let there is filtration flow due to some external cautions and there are roots of plants which are perpendicular to a plane
of saturated porous media. Let there is filtration flow due to some external cautions and there are roots of plants which are perpendicular to a plane 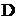 . The roots of plants create locally decreased pressure due to osmotic effect and, as a result, they suck up water. Cross-section areas of roots of plants are negligibly small. Then the filtration flow is described by following equation:
. The roots of plants create locally decreased pressure due to osmotic effect and, as a result, they suck up water. Cross-section areas of roots of plants are negligibly small. Then the filtration flow is described by following equation:
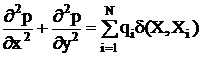 , (1)
, (1)
 , (2)
, (2)
where 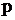 is pressure in porous media;
is pressure in porous media; 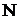 is number of roots of plants;
is number of roots of plants;  are intensities of sinks;
are intensities of sinks; 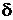 is Dirac's delta-function;
is Dirac's delta-function; 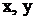 are Cartesian coordinates,
are Cartesian coordinates,  is point of domain
is point of domain 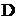 ,
, 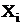 is position of the root of plant;
is position of the root of plant; 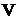 is velocity of the filtration flow;
is velocity of the filtration flow; 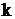 is filtration coefficient. Correspondent boundary conditions are prescribed on the boundary
is filtration coefficient. Correspondent boundary conditions are prescribed on the boundary 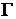 of the domain
of the domain 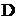 for equation (1). Intensity of sink
for equation (1). Intensity of sink  depends on osmotic pressure, created by correspondent root of plant and local "pressure in infinity". The last term means the pressure in position of the sink, if the sink is absent there. The simplest dependence of
depends on osmotic pressure, created by correspondent root of plant and local "pressure in infinity". The last term means the pressure in position of the sink, if the sink is absent there. The simplest dependence of  on pressure is, of course, linear, what provides completely linear filtration problem. However, such non-linear dependences are possible too, that leads to evident mathematical and computational difficulties.
on pressure is, of course, linear, what provides completely linear filtration problem. However, such non-linear dependences are possible too, that leads to evident mathematical and computational difficulties.
Presence of delta- functions in the formulation of problem (1) makes it multiscale. As a result, the most popular finite difference and finite element methods can not be applied for its numerical solution. Thus boundary element method is the only tool, that can be used here. To apply a boundary element method, let us transform the initial governing differential equation to boundary integral equation:
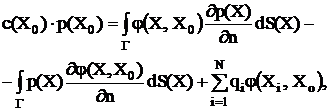 (3)
(3)
where 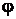 is fundamental solution of Laplace equation;
is fundamental solution of Laplace equation; 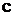 is function of boundary shape.
is function of boundary shape.
Equetion (3) can be solved by usual boundary element algorithm with only difference in last term in right hand side of equation if 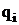 linear depends on
linear depends on 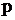 , equation (3) can be approximated by system lineal algebraic equations, including additional equations for determinations of unknown values
, equation (3) can be approximated by system lineal algebraic equations, including additional equations for determinations of unknown values 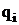 In the case of non-linear dependence, equations for
In the case of non-linear dependence, equations for 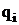 are non-linear and require a special iteration process to handle them.
are non-linear and require a special iteration process to handle them.
Let us consider some substance transfer by filtration flow. It is described by following equation
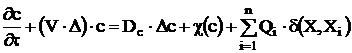 , (4)
, (4)
where 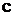 is concentration of transferred substance;
is concentration of transferred substance; 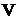 is filtration velocity;
is filtration velocity; 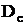 is diffusion coefficient; the second term in right hand ride of equation (4)
is diffusion coefficient; the second term in right hand ride of equation (4)  describes sorption process, that is this term represents distributed sources (sinks); the last term in right hand side of equation (4) corresponds to the mentioned effect of roots of plants.
describes sorption process, that is this term represents distributed sources (sinks); the last term in right hand side of equation (4) corresponds to the mentioned effect of roots of plants.
Equation (4) with necessary initial and boundary conditional is multiscale problem, but this case requires completely another approach. The following spitting

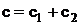 (5)
(5)
gives an opportunity to avoid computational difficulties. Concentration 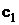 corresponds to distributed sources and it is described by transfer equation like (4) without the last term. Concentration
corresponds to distributed sources and it is described by transfer equation like (4) without the last term. Concentration 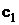 field can be calculated by usual finite deferens method, for example, explicit “up-wined” scheme is used in the present work:
field can be calculated by usual finite deferens method, for example, explicit “up-wined” scheme is used in the present work:
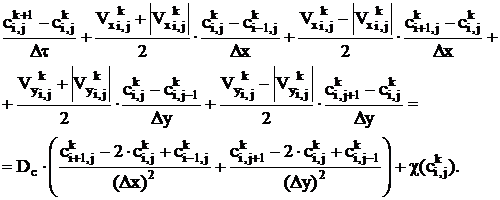 (6)
(6)
Concentration 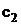 corresponds to localized sources (sinks) and it can be analyzed by potential theory methods. For example, this field can be approximated by sum of fundamental solution of Oseen’s equation.
corresponds to localized sources (sinks) and it can be analyzed by potential theory methods. For example, this field can be approximated by sum of fundamental solution of Oseen’s equation.
The proposed approach is illustrated by several examples of numerical calculations, which conforms its workability and effectiveness.
 of saturated porous media. Let there is filtration flow due to some external cautions and there are roots of plants which are perpendicular to a plane
of saturated porous media. Let there is filtration flow due to some external cautions and there are roots of plants which are perpendicular to a plane  . The roots of plants create locally decreased pressure due to osmotic effect and, as a result, they suck up water. Cross-section areas of roots of plants are negligibly small. Then the filtration flow is described by following equation:
. The roots of plants create locally decreased pressure due to osmotic effect and, as a result, they suck up water. Cross-section areas of roots of plants are negligibly small. Then the filtration flow is described by following equation: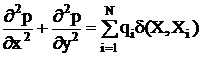 , (1)
, (1)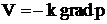 , (2)
, (2)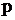 is pressure in porous media;
is pressure in porous media; 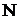 is number of roots of plants;
is number of roots of plants;  are intensities of sinks;
are intensities of sinks; 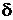 is Dirac's delta-function;
is Dirac's delta-function; 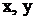 are Cartesian coordinates,
are Cartesian coordinates,  is point of domain
is point of domain 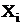 is position of the root of plant;
is position of the root of plant; 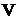 is velocity of the filtration flow;
is velocity of the filtration flow; 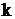 is filtration coefficient. Correspondent boundary conditions are prescribed on the boundary
is filtration coefficient. Correspondent boundary conditions are prescribed on the boundary 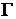 of the domain
of the domain 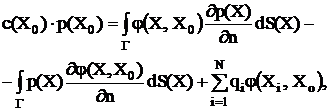 (3)
(3) 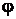 is fundamental solution of Laplace equation;
is fundamental solution of Laplace equation; 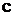 is function of boundary shape.
is function of boundary shape.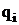 linear depends on
linear depends on 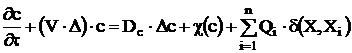 , (4)
, (4)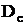 is diffusion coefficient; the second term in right hand ride of equation (4)
is diffusion coefficient; the second term in right hand ride of equation (4)  describes sorption process, that is this term represents distributed sources (sinks); the last term in right hand side of equation (4) corresponds to the mentioned effect of roots of plants.
describes sorption process, that is this term represents distributed sources (sinks); the last term in right hand side of equation (4) corresponds to the mentioned effect of roots of plants.
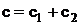 (5)
(5)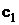 corresponds to distributed sources and it is described by transfer equation like (4) without the last term. Concentration
corresponds to distributed sources and it is described by transfer equation like (4) without the last term. Concentration 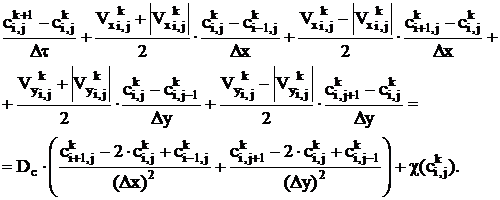 (6)
(6)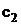 corresponds to localized sources (sinks) and it can be analyzed by potential theory methods. For example, this field can be approximated by sum of fundamental solution of Oseen’s equation.
corresponds to localized sources (sinks) and it can be analyzed by potential theory methods. For example, this field can be approximated by sum of fundamental solution of Oseen’s equation.