Kochubey O. O., Yevdokymov D. V., Kriachunenko O. L., Goncharenko M. P.
Oles Honchar Dnipropetrovsk National University
ONE MATHEMATICAL MODEL OF MULTIPHASE FLOW IN SMALL DOMAIN
At present time, fast development of microelectronics, micromechanics and microbiology stimulates constantly growing interests to different mechanical effects in liquid media in small domains. Multiphase flows are always considered as the most sophisticated and difficult in fluid dynamics. It is quite natural, that multiphase flows represent a lot of difficulties on small size level. However such multiphase flows have some specific features in comparison with usual multiphase flows. First of all, number of the second phase objects is very restricted due to small size of domain. Thus, traditional average mathematical model of multiphase flows can not be used in this case and only Lagrangian approaches remain applicable. The second specific feature is Stokes flow taking place there instead of usual Navier-Stokes flow due to small reference size of domain. Multiphase Stokes flour with Lagrangian treatment of the second phase is rather new hydrodynamic problem. The aim of the presented work is to develop a solution technique for the considered problem.
It is well known from multiphase flow theory, that surface forces are sufficiently dominative in comparison with body forces for asymptotically small bodies, including inertia force. Consequently asymptotically small particle always moves under force equilibrium. If particles are small in comparison with referent size of small domain, they can be classified as extremely small. Thus, the above conclusion takes place in the considered case. This circumstance gives an opportunity to simplify the problem and to replace dynamic analysis of particle motions by kinematic analysis.
Let us consider small domain 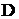 , which contains a liquid with restricted number of spherical particles. Let us assume that there is some Stokes flow stimulated by external cautions in domain
, which contains a liquid with restricted number of spherical particles. Let us assume that there is some Stokes flow stimulated by external cautions in domain 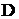 . Smallness of the domain
. Smallness of the domain 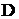 . means that its reference size is so small to provide
. means that its reference size is so small to provide 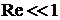 (Reynolds number is introduced by usual way as
(Reynolds number is introduced by usual way as 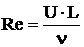 ), that, of course, requires correspondent reference velocity
), that, of course, requires correspondent reference velocity 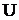 .
.
Following forces are acting on particles:
- gravitational force 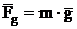 ;
;
- Archimedes force 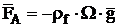 ;
;
- possible other body forces, for example, electromagnetic force; all mass forces are assumed known and known summarized body force 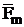 can be introduced;
can be introduced;
- thermophoretic and diffusiophoretic force determined by following formula:
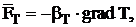 (1)
(1)
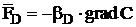 , (2)
, (2)
where 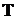 and
and 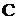 are corresponding temperature of the liquid and concentration of saluted substance:
are corresponding temperature of the liquid and concentration of saluted substance:
- vicious dray force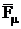 ;
;
- hydrodynamic interaction force 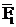 .
.
For the sake of simplicity, a lot of physical phenomena; like Magnus force and Safmen force, are not considered here.
Generally speaking, all unknown forces can be obtained from solution of correspondent boundary value problem for Stokes equation system:
 (3)
(3)
However, even numerical solution of boundary-value problem for system (3) with direct calculation of flow around every particle is completly impossible from computational point of view. That is why some simplifications and approximations must be used here. In particular, the following splitting with respect to physical processes is suitable to use in the considered case
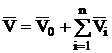 , (4)
, (4)
where 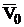 is velocity field in the domain D due to external cautions, calculated without taking into account of particles;
is velocity field in the domain D due to external cautions, calculated without taking into account of particles;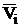 are solutions of Stokes problem for spherical particle in unbounded space. All solutions
are solutions of Stokes problem for spherical particle in unbounded space. All solutions 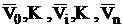 identically satisfy to system (3), but they do not satisfy to boundary conditions, that requires to organize an additional iteration process or to include additional arbitrariness with additional conditions for their determinations into the formulation. Note that an analytical solution for Stokes flow around a ball, which is well known [1], can be used here for
identically satisfy to system (3), but they do not satisfy to boundary conditions, that requires to organize an additional iteration process or to include additional arbitrariness with additional conditions for their determinations into the formulation. Note that an analytical solution for Stokes flow around a ball, which is well known [1], can be used here for 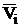 construction. Velocity
construction. Velocity 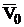 can be calculated by any numerical method, for example, boundary element method.
can be calculated by any numerical method, for example, boundary element method.
To complete a description of algorithm, it is necessary to consider motions of the particles. The force equilibrium condition is
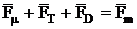 . (5)
. (5)
Since we deal with spherical particles, Stokes formula takes place in this case:
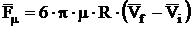 , (6)
, (6)
where 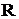 is radius of particle;
is radius of particle; 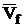 is flow velocity in point, where the particle is situated, under assumptive that the particle is absent there. Thus
is flow velocity in point, where the particle is situated, under assumptive that the particle is absent there. Thus
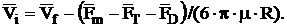 (7)
(7)
The equation system (7) with correspondent boundary conditions can be considered as Cauchy problem for determination of particle motions:
 (8)
(8)
To make the analysis easy and clear, the simplest mathematical models for temperature and concentration fields are used here:
 , (9)
, (9)
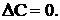 (10)
(10)
Boundary-value problems, created by equations (9), (10) and correspondent boundary conditions, can be solved by any numerical method, for example, boundary element method is used here.
The proposed approach is illustrated by several examples of numerical calculations, which conforms its workability and effectiveness.
The list of references:
1. Happel J., Brenner H. Low Reynolds number hydrodynamics. – L.: Prentice-Hall, 1965.
 , which contains a liquid with restricted number of spherical particles. Let us assume that there is some Stokes flow stimulated by external cautions in domain
, which contains a liquid with restricted number of spherical particles. Let us assume that there is some Stokes flow stimulated by external cautions in domain 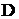 . Smallness of the domain
. Smallness of the domain 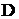 . means that its reference size is so small to provide
. means that its reference size is so small to provide 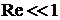 (Reynolds number is introduced by usual way as
(Reynolds number is introduced by usual way as 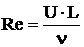 ), that, of course, requires correspondent reference velocity
), that, of course, requires correspondent reference velocity 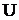 .
.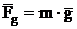 ;
;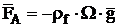 ;
;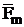 can be introduced;
can be introduced;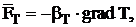 (1)
(1)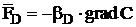 , (2)
, (2)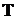 and
and 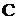 are corresponding temperature of the liquid and concentration of saluted substance:
are corresponding temperature of the liquid and concentration of saluted substance: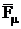 ;
;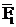 .
. (3)
(3)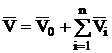 , (4)
, (4)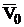 is velocity field in the domain D due to external cautions, calculated without taking into account of particles;
is velocity field in the domain D due to external cautions, calculated without taking into account of particles;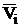 are solutions of Stokes problem for spherical particle in unbounded space. All solutions
are solutions of Stokes problem for spherical particle in unbounded space. All solutions 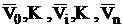 identically satisfy to system (3), but they do not satisfy to boundary conditions, that requires to organize an additional iteration process or to include additional arbitrariness with additional conditions for their determinations into the formulation. Note that an analytical solution for Stokes flow around a ball, which is well known [1], can be used here for
identically satisfy to system (3), but they do not satisfy to boundary conditions, that requires to organize an additional iteration process or to include additional arbitrariness with additional conditions for their determinations into the formulation. Note that an analytical solution for Stokes flow around a ball, which is well known [1], can be used here for 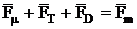 . (5)
. (5)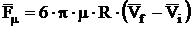 , (6)
, (6)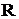 is radius of particle;
is radius of particle; 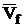 is flow velocity in point, where the particle is situated, under assumptive that the particle is absent there. Thus
is flow velocity in point, where the particle is situated, under assumptive that the particle is absent there. Thus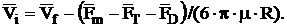 (7)
(7) (8)
(8) , (9)
, (9)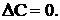 (10)
(10)