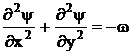 , (1)
, (1)Kochubey O. O., Yevdokymov D. V., Kriachunenko O. L., Morenko M. S.
Oles Honchar Dnipropetrovsk National University
NUMERICAL ANALYSIS OF AIR POLLUTION TRANSFER BY COMBINED METHODS
Modern stage of human activity demonstrates an evidently increasing dependence of human life quality on environment situation. Growing number of problems with human health are explained by negative ecological actions, stimulated by human industrial and agricultural activity. Mainly ecological danger is connected with air, water and soil pollutions. The term “pollution” is determined by usual way as non-specific introduction of some chemical substances, including radioactive substances, into environmental media in non-specific amounts. In spite of clear understanding of ecological danger, that have been stimulated by some political and social ecological movements, and huge efforts of governments, as well as special organizations, ecological problems remain extremely serious and unsolved.
Let us consider reasons of such situation. First of all, ecological theories on modern stage of their developments remain “qualitative sciences”. The last conclusion means that real mechanisms of influences of environment on human health still remain unknown. We only know that human organism has some adaptive opportunities, that provide quite wide boundaries for “normal life”. Beside of that, there are sufficient differences between long-time and short-time negative environmental actions. However all mentioned effects remain almost completely unclear of ecological sciences. The so-called limit concentrations were determined on the base of pure understanding of the considered phenomena, nevertheless the mentioned limit concentrations are defined in legislations of many countries. More than that, we don’t know the answer to main question of modern ecology: is some specific problem with human health caused by influence of specific pollution, or by action of other pollution, or by combined action of several pollutions, or by completely other negative tendencies in human life? Thus, creation of quantitative ecological theory must be considered as a main aim of ecological sciences at nowadays.
Investigations of pollution transfers, united by name of “computational ecology”, are based on well-known approaches of computational fluid dynamics and successfully developed since approximately 1960 using the same computational devises that are finite difference and finite element method software. As a result, a lot of problems about pollution transfer in regional and subregional scales were successfully solved numerically by the mentioned software. However from the very beginning of such investigations; it was clear, that linear sizes of pollution sources are sufficiently less, than correspondent sizes of solution domains. In fact, it was classical multiscale problem, but a proper attention was not paid to this circumstance. To avoid this difficulty, the source of pollution was distributed on one or several finite difference cells (one or several finite elements), that was physically incorrect, but it provided quite good numerical results on regional scales. Natural mathematical model of local pollution source is, of course, Dirak’s delta-function, but such formulation requires a consideration and solution in generalized function spaces, that is completely impossible for finite difference and finite element methods. At the moment, pollution concentration distributed near the pollution source attracts main interest. Especially it is important for investigation of air pollution transfer in cities and industrial districts, where a lot of sources are located and pollution concentrations must be calculated near the sources. Thus, finite difference method and finite element method cannot provide proper accuracy of pollution transfer calculation and must be replaced by same other numerical method.
Since multiscale problems in complex geometrical shape domains are considered, it is quite natural to apply for their numerical solution methods of computational potential theory. However, well-known disadvantages of computational potential theory in transfer problems for distributed fields made this group of numerical methods ineffective for the considered kind of problems.
The aim of the present work is to analyze an opportunity of development of combined numerical method for solution of the considered problem. The main idea of combined numerical method is the splitting of vorticity field and concentration fields into localized fields and distributed fields. The localized fields are calculated by Lagrangian algorithms of computational potential theory and distributed fields are calculated by usual finite difference method.
Let us formulate the fluid flow problem in term “vorticity – stream function” in dimensionless form. For the sake of simplicity let us restrict the following consideration by a plane case.
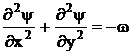 , (1)
, (1)
 . (2)
. (2)
Here all notations are used in traditional senses. Reynolds number is introduced by usual way 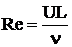 , but the kinematic viscosity
, but the kinematic viscosity 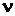 can be physical coefficient of viscosity or effective coefficient of turbulent viscosity. For ideal fluid flow following equation must be used instead equation (2):
can be physical coefficient of viscosity or effective coefficient of turbulent viscosity. For ideal fluid flow following equation must be used instead equation (2):
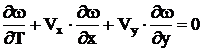 . (3)
. (3)
Substance concentration transfers are described by following equations:
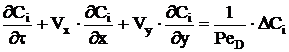 . (4)
. (4)
The formulated above equations must be complemented by proper initial and boundary conditions.
According to potential theory equation (1) must be replaced by following boundary integral equation [1]:
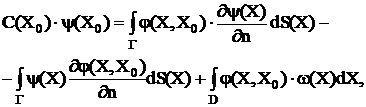 (5)
(5)
where 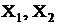 are point of plane, function C is boundary shape function, determined in [1],
are point of plane, function C is boundary shape function, determined in [1], 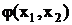 is fundamental solution of Laplace equation.
is fundamental solution of Laplace equation.
Splitting into localized and distributed field is following:
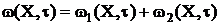 , (6)
, (6)
 , (7)
, (7)
where
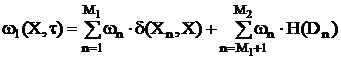 , (8)
, (8)
here 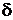 is Dirahin delta-function, H is Heaviside’s function of domain,
is Dirahin delta-function, H is Heaviside’s function of domain,
 . (9)
. (9)
Motions of the objects introduced by relations (8),(9) are described by Cauchy problem for following system of ordinary differential equations
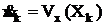 , (10)
, (10)
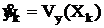 .
.
Points 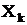 in equation (10) are either points, where discrete vortices are situated, or representative points of boundaries of localization domains. The last trick is similar to contour dynamics method. Components of velocity
in equation (10) are either points, where discrete vortices are situated, or representative points of boundaries of localization domains. The last trick is similar to contour dynamics method. Components of velocity 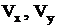 in (10) are obtained by direct differentiation from (5). The distributed fields
in (10) are obtained by direct differentiation from (5). The distributed fields 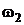 and
and 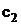 are continuous in domain
are continuous in domain 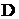 functions. Transfers of the mentioned fields are described by equations (3), (4) and can be calculated using some finite difference scheme. For example, an explicit up-wind scheme on rectangular grid is used for numerical calculation in present work.
functions. Transfers of the mentioned fields are described by equations (3), (4) and can be calculated using some finite difference scheme. For example, an explicit up-wind scheme on rectangular grid is used for numerical calculation in present work.
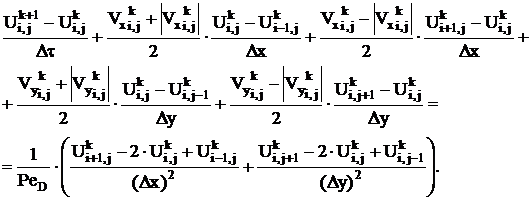 (11)
(11)
All notations in finite difference scheme (11) are used in usual sense.
The proposed approach is illustrated by several examples of numerical calculations, which conforms its workability and effectiveness.
The list of references:
1. Yevdokymov D.V. Boundary element and discrete vortices method for ideal fluid flow calculations. in D. Durban and A.R.J. Pearson (Eds.) Non-linear singularities in deformation and flow. Proceeding of IUTAM Symposium held in Haifa, Israel, 17-21 March, 1997. Kluwer Academic Publisher. – Р. 217–230.