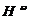 OF SPACES
OF SPACES 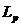 (p = 4)
(p = 4)Konovalov E. O., Chernitska O. V., Atanova M. J.
Oles Honchar Dnipropetrovsk National University
APPLICATION OF KORNIYCHUK 'S INEQUALITY TO THE UPPER BOUND DIMENSIONAL LINEAR WIDTHS
SUBCLASS 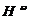 OF SPACES
OF SPACES 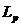 (p = 4)
(p = 4)
Inequality which is valid for all 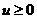 for
for 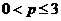 was established and proven by M.P Korniychuk [1, p. 225-226]:
was established and proven by M.P Korniychuk [1, p. 225-226]:
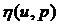 =
=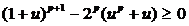 . (1)
. (1)
Inequality is examined for significance 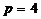 . The continuous function f(t),
. The continuous function f(t),  [а,b] is considered and has the view such as on the drawing (Fig. 1).
[а,b] is considered and has the view such as on the drawing (Fig. 1).
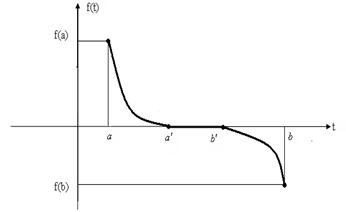
Fig. 1. Function f(t)
Function 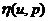 becomes negative in the intervals
becomes negative in the intervals 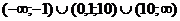 . If you want to do the inequality (1) correct, you will require compliance next equality:
. If you want to do the inequality (1) correct, you will require compliance next equality:
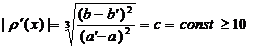 . (2)
. (2)
So, if function f(t) such as on the drawing, for p=4 and 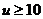 , next inequality will correct:
, next inequality will correct:
 , (3)
, (3)
where 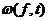 – is the modulus of continuity of function f(t).
– is the modulus of continuity of function f(t).
The list of references:
1. Korneychuk N. P. Splines in theory of approximations. – M.: Science, Home edition physical and mathematical literature, 1984. – 352 p.