Iopel D., Bilan S., Goncharova Y.
Oles Honchar Dnipropetrovsk National University
DETERMINING THE DISTRIBUTION NETWORK STRUCTURE TAKING INTO ACCOUNT THE REAL POSSIBILITIES OF WAREHOUSE PLACEMENT
Topicality of the problem. The task of determining the locations of storage capacities on the criterion of transport costs is one of the fundamental problems of logistics. The founders of this research were A. Weber and J. Peak in the “Theory of the Location of Industries”, (1909). But nowadays the problem of determining the structure of the warehouse network remains urgent.
Goal of Research – the algorithm design of determining the effect of the number of warehouses for logistics transportation costs based on real transport communications and possiblelocations of distribution centers.
The presentation of the basic material of the research. Suppose that there are M suppliers (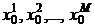 ) and J consumers (
) and J consumers (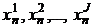 ). Within the precincts of a city there are Koptions for placement of storage capacities (
). Within the precincts of a city there are Koptions for placement of storage capacities (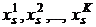 ). Crossroads of the city are marked
). Crossroads of the city are marked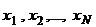 . Graph G, corresponding to the transport network, is defined by the table, in which a path length from the vertex
. Graph G, corresponding to the transport network, is defined by the table, in which a path length from the vertex 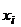 to
to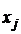 is situated at the intersection of i-th row and j-th column, if these vertices are adjacent.
is situated at the intersection of i-th row and j-th column, if these vertices are adjacent.
At the preliminary stage it is necessary to find all shortest paths between all vertices. This problem can be solved, for example, using the Dantzig's algorithm [4, p.58]. Received distances between each pair of vertices are entered into the data set and hereafter a chunk of received array is used at each stage.
In addition the database is formed:
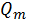 – the amount of products supplied by m-th enterprise (
– the amount of products supplied by m-th enterprise (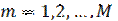 );
);
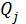 – the volume of production required by j-th customer (
– the volume of production required by j-th customer (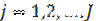 );
);
С0 – the transport tariff, cu. / km;
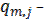 the rated capacity of rolling stock used for the transport from the m-th supplier to the j-th customer, T;
the rated capacity of rolling stock used for the transport from the m-th supplier to the j-th customer, T;
the coefficient of capacity of the rolling stock used for transportation from the m-th supplier to the j-th customer.
To account the additional factors that influence on the plan of optimal consolidation of customers around suppliers (the impossibility of direct deliveries, consumer preferences in the selection of suppliers, etc.), weight fractions m-th supplier 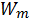 and j-th consumer
and j-th consumer 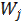 are entered.
are entered.
The first stage. Traditionally, the task of fixing the transport suppliers for consumers in the presence of two or more warehouses is solved twice – from M suppliers to K warehouses and from K warehouses to J consumers. If the warehouse is only one then for minimization of transportation costs it is enough to select warehouse corresponding to the vertex, for which:
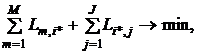
where  ,
,  – the shortest paths from suppliers
– the shortest paths from suppliers 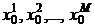 to warehouse
to warehouse 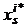 and from warehouse
and from warehouse 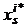 to consumers
to consumers 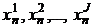 . In this case, the total cost for transportation S can be calculated by the formula:
. In this case, the total cost for transportation S can be calculated by the formula:
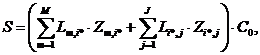
where 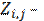 the number of loaded trips between places and that is calculated by the next formula:
the number of loaded trips between places and that is calculated by the next formula:
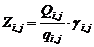 . (1)
. (1)
The second stage. Warehouse positioning. The vertex, selected in the first stage, is determined as “basic”.
Then the next magnitude 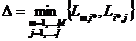 is determined. Next vertices from the vertex
is determined. Next vertices from the vertex 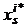 are taken into consideration no more than distance
are taken into consideration no more than distance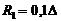 . First, two peaks in oppositedirections are taken, then two, etc. If in circle of the radius
. First, two peaks in oppositedirections are taken, then two, etc. If in circle of the radius 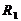 there is only one vertex that is different from
there is only one vertex that is different from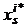 then it is viewed as the second, solving the problem of fixing suppliers forconsumers and determining the logistics transportation costs.
then it is viewed as the second, solving the problem of fixing suppliers forconsumers and determining the logistics transportation costs.
Thereafter, vertices, situated from "basic" at a distance over 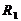 and no more than
and no more than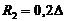 , then at a distance
, then at a distance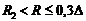 , etc., are taken into consideration.
, etc., are taken into consideration.
The third stage. Calculation of minimum total costs of transportation at different locations of warehouses.
In the presence of two or more warehouses it is necessary to determine the volume of transportations from suppliers to warehouses and from warehouses to customers, minimizingtransportation work P (m × km). Thus, the objective function will be:
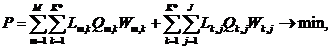
where m=1, 2,…, M – suppliers; k=1, 2,…,K* (K*≥2) – warehouses, selected in the second stage; j=1, 2,…, J – consumers;
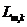 and
and 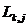 – the distances from the m-th supplier to the k-th warehouse and from the k-th warehouse to the j-th consumer;
– the distances from the m-th supplier to the k-th warehouse and from the k-th warehouse to the j-th consumer;
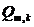 and
and 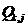 – unknown volumes of cargo transportation from the the m-th supplier to the k-th warehouse and from the k-th warehouse to the j-th consumer, respectively;
– unknown volumes of cargo transportation from the the m-th supplier to the k-th warehouse and from the k-th warehouse to the j-th consumer, respectively;
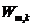 and
and 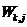 – weight fractions from the m-th supplier to the k-th warehouse and from the k-th warehouse to the j-th consumer, respectively.
– weight fractions from the m-th supplier to the k-th warehouse and from the k-th warehouse to the j-th consumer, respectively.
After determining the volume of traffic from suppliers to warehouses and from warehouses to consumers the logistics transportation costs are calculated as follows:
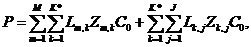
where the number of loaded trips 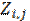 is defined by (1).
is defined by (1).
The resulting database of the traced analysis of the amount of transportation costs and the location of the warehouse can be used to make a decision on the formation of the optimal warehouse network with the available options for the location of distribution centers. As well, the represented algorithm can be used to select the locations for additional warehouses in the expansion of the distribution system.
The solution to the above problem is quite time-consuming, requires the use of computer systems and assistance of an operator during the choosing of opposite located vertices.
Conclusion. The represented algorithm can be applied when the objects are set not by Cartesian coordinates, but the actual distance between them, and when you need to consider reallypossible location of the storage capacity.
The list of references:
1. Гаджинский А. М. Выбор места расположения склада [Електронный ресурс]/ А. М. Гаджинский // Справочник экономиста. – 2004. – №8.– Режим доступа: http://www.profiz.ru/se/8-2004.
2. Мадера А. Г. Определение оптимального размещения логистических мощностей [Електронный ресурс] / А. Г. Мадера. – Режим доступа: http://www.sklada.ru.
3. Іванов Р. В. Про методику визначення місця розташування розподільного центру / Р. В. Іванов, С. О. Білан // Вісн. Дніпропетр. нац. ун-ту. Серія Економіка. – 2009. – Т.17. – №10/1.– Вип. 3(2). – С. 147–151.
4. Майника Э. Алгоритмы оптимизации на сетях и графах : пер. с англ./ Э. Майника. – М.: Мир, 1981. – 328 с.
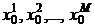 ) and J consumers (
) and J consumers (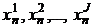 ). Within the precincts of a city there are Koptions for placement of storage capacities (
). Within the precincts of a city there are Koptions for placement of storage capacities (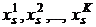 ). Crossroads of the city are marked
). Crossroads of the city are marked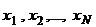 . Graph G, corresponding to the transport network, is defined by the table, in which a path length from the vertex
. Graph G, corresponding to the transport network, is defined by the table, in which a path length from the vertex 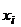 to
to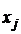 is situated at the intersection of i-th row and j-th column, if these vertices are adjacent.
is situated at the intersection of i-th row and j-th column, if these vertices are adjacent.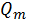 – the amount of products supplied by m-th enterprise (
– the amount of products supplied by m-th enterprise (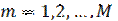 );
);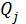 – the volume of production required by j-th customer (
– the volume of production required by j-th customer (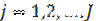 );
);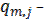 the rated capacity of rolling stock used for the transport from the m-th supplier to the j-th customer, T;
the rated capacity of rolling stock used for the transport from the m-th supplier to the j-th customer, T;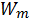 and j-th consumer
and j-th consumer 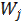 are entered.
are entered.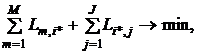
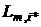 ,
, 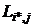 – the shortest paths from suppliers
– the shortest paths from suppliers 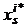 and from warehouse
and from warehouse 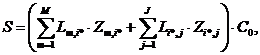
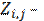 the number of loaded trips between places and that is calculated by the next formula:
the number of loaded trips between places and that is calculated by the next formula: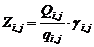 . (1)
. (1)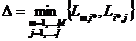 is determined. Next vertices from the vertex
is determined. Next vertices from the vertex 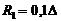 . First, two peaks in oppositedirections are taken, then two, etc. If in circle of the radius
. First, two peaks in oppositedirections are taken, then two, etc. If in circle of the radius 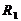 there is only one vertex that is different from
there is only one vertex that is different from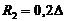 , then at a distance
, then at a distance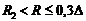 , etc., are taken into consideration.
, etc., are taken into consideration.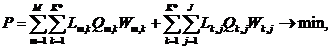
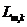 and
and 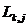 – the distances from the m-th supplier to the k-th warehouse and from the k-th warehouse to the j-th consumer;
– the distances from the m-th supplier to the k-th warehouse and from the k-th warehouse to the j-th consumer;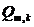 and
and 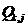 – unknown volumes of cargo transportation from the the m-th supplier to the k-th warehouse and from the k-th warehouse to the j-th consumer, respectively;
– unknown volumes of cargo transportation from the the m-th supplier to the k-th warehouse and from the k-th warehouse to the j-th consumer, respectively;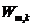 and
and 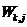 – weight fractions from the m-th supplier to the k-th warehouse and from the k-th warehouse to the j-th consumer, respectively.
– weight fractions from the m-th supplier to the k-th warehouse and from the k-th warehouse to the j-th consumer, respectively.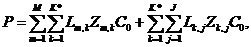
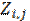 is defined by (1).
is defined by (1).