Baboshkin I. I., Kuzmenko V. І., Аtаnоvа М. Y.

Oles Honchar Dnipropetrovsk National University

COMPUTER MODELING OF MASSIVE STRUCTURES BEHAVIOR ON HETEROGENEOUS BASES

Nowadays building must be carried out on heterogeneous bases. That is why it is very important to carry out a research of non-uniform settlings which appears as the result of bases’ heterogeneity. Important results were received for elastoplastic multilayer bases in work [1].

Plane deformation of heterogeneous band is being researched. The properties of the band are described by Lamé parameters l and m in each point of the band. The band is being deformed under the influence of the massive stamp with a flat foundation. As a result of the band deformation the stamp receives vertical shift (settling) D and rotation j, that are considered to be given (Fig. 1).

Fig. 1. Rotation and shift of the stamp

The problem is to find components of displacement vector 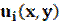, small deformation tensor  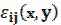and stress tensor 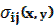. Mentioned characteristics have to satisfy equations of equilibrium, Cauchy relations and determinative relations. Moreover, conditions

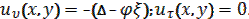
must be satisfied on contact area of the stamp and the band.

Extremal variational problem for the specified problem was received using typical method given in [2]:

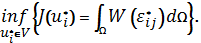
For discretization of the problem was used finite-element mesh. We received a linear system of equations that was solved using method of successive over-relaxation (SOR). To get stamp’s settlings by its weight we solve nonlinear equation

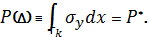
Built model also takes into consideration creep [4].

We got the following results:

1. The numerical solution of given problem was received. The practical convergence of approximated solutions was shown.

2. The relation between settlings and creep properties of the band was shown. The relation between contact stresses and band thickness.

3. The results can be applied for evaluation of buildings’ settlings and rotations on heterogeneous bases.

The list of references:

1. Власенко Ю. Г. Взаимодействие тяжелых штампов с многослойным упруго­пластическим основанием, содержащим включения: Дис. … канд. тех. наук: спец. 05.23.17 «Строительная механика» / Ю. Г. Власенко. – Д., 2010. – 151 с.

2. Кузьменко В. И. Решение на ЭВМ задач пластического деформи­рования: Справочник / В. И. Кузьменко, В. Ф. Балакин. – К.: Тэхника. – 136 с.

3. Кузьменко В. І. Вступ до методів скінченних елементів / В. І. Кузь­менко. – Д.: РВВ ДНУ, 2002. – 84 с.

4. Малинин Н. Н. Прикладная теорія пластичности и ползучести / Н. Н. Ма­линин. –  М.: Машиностроение, 1975. – 400 с.