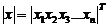near the smoothed delta functions:Tovstick A., Petrenko A., Timoshenko Z.
Oles Honchar Dnipropetrovsk National University
STATISTICAL PROCESSING OF ULTRASONIC NONDESTRUCTIVE TESTING WITH HONEYCOMB STRUCTURE
At present more often increasingly composites are being used in various industries. So, they are used in the aerospace industry to reduce the weight of aircraft. For example, the usage percentages of fiber-reinforced composite materials in the latest Boeing B787 and newly-designed Airbus A350-XWB reach 50% and 52%, respectively.. One of the most used composites is honeycomb structures.
Honeycomb structures are mostly sandwich. They consist of such parts: the upper casing and the lower casing and honeycomb core between them. Honeycomb fillers possess high performance stability and considerable rigidity to bending.
Manufacturing technology is the following. Parallel strips of glue are applied on paper impregnated monomer; sheets glued to a thick block, alternate strips of adhesive, block stretched honeycomb, after which the monomer undergoes polymerization honeycomb plate is glued between sheets of plywood, plastic or metal, forming a sandwich-like structure.
The main type of defects in the manufacture is a bundle sheathing of honeycomb panels and non-glued cladding to honeycomb core. At present, almost all methods of monitoring cellular panels are directed to the discovery of bundles. The main types of controls that are used, is a thermal control, a holographic control, ultrasonic inspection.
So, there are several types of ultrasonic testing techniques: impedance method, free vibration, echo method and the shadow method.
Ultrasonic nondestructive testing is the most commonly used. However, for high-quality data processing it is necessary to use information technology. As a result, of control get the sample of measurements. Some sample measurements are obtained also known are that characterize the normal state of the object and Defective condition.
It is necessary to define modalities under which the indicators are used to assess the effectiveness of recognition when the maximum and minimum values will take place. Working patterns are different types of PKM: plating, stainless steel and aluminum honeycomb, Kevlar and paper honeycomb paneling and others.
For monitoring of composite materials flaw detector UD2-16 is proposed. This flaw detector is used to manually control the echo, shadow and mirror-shadow method, and can be used in thin-route control mechanized units. It allowed finding defects, such as continuity and uniformity, non-glued layers. In particular, with the help of this flaw detector, the honeycomb structure with non-contact ultrasonic shadow was control. This type of control provides high accuracy, since the method does not have the deep uncontrolled area.
For managing, analyzing and mathematical treatment of the results acoustic control, "portraits" working samples were made. Acoustic "portrait" is a special matrix, where the maximum amplitude of the ultrasonic signals passing through the sample was taken. These signals were recorded by flaw detector. Heterogeneity and discontinuity of the composite material has a significant influence on the amplitude of the received ultrasonic signal. The acoustic "portrait" was carried out in seven-color changing colors with a resolution of 60 mV was taken for comfort study. This portrait contains information on the physical and mechanical properties of the sample and its integrity.
To assess the quantitative characteristics of the acoustical transparency of the sample the arithmetic mean value of the received amplitude and the average attenuation was also detected.
This technique allows the processing of the information to identify the most likely defects such as non-glued in conjunction honeycomb paneling, or delamination in the hull, as well as to judge the development of work processes in the manufacture of FRP with honeycomb core.
For assessing effectiveness it is proposed the decision rule formulated by the smoothed delta functions.
Let us formulate decision rule on the status of cellular structures with recovery the laws of distribution smoothed delta functions.
In this expression, the function under the limit is called the smoothed delta function. If now in terms of the Dirac delta function is replaced by a smoothed delta function, we can express the unknown probability distribution law with a sample of 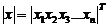near the smoothed delta functions:
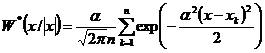(1)
α – he smoothing parameters.
In real conditions the control sample measurements satisfy the inequality: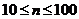 
. Using a linear approximation of the dependence we get formulas for estimating the smoothing parameters.
Estimates of the expectation and estimate of the variance were also determined.
Probability distribution law is restored by the formula and it is determined the decision rule.
The conditional probability of error is determined by the conditional probability of making rules (P11 *) as the norm for marriage and marriage (P22 *), Efficiency of recognition (P).
The studies were conducted in a software environment MathCad.
After studding, it is clear that this Method to recognize is very convenient because it does not require knowledge of the laws of probability distributions, which allows determining only informative indicators. The conditional probabilities in the research and their effectiveness are high levels. It should be noted that the greater the number of measurements in the sample, the more effective exponential estimates of probabilities.
The list of references:
1. Братухин А. Г. Технология производства изделий и интегральных конструкций из композитных материалов в машиностроении / А. Г. Братухин, В. С. Боголюбов, О. С. Сироткин. – М.: Готика, 2003. – 516 с.
2. Малайчук В. П. Математична дефектоскопія / В. П. Малайчук, А. В. Мозговий. – Дніпропетровськ: Системні технології, 2005. – 179 с.
3. Малайчук В. П. Інформаційно-вимірювальні технології неруйнівного контролю / В. П. Малайчук, А. В. Мозговий. – Дніпропетровськ: РВВ ДНУ, 2001. – 237с.
4. Малайчук В. П. Обробка вимірювань і сигналів неруйнівного контролю / В. П. Малайчук, О. М. Петренко. – Дніпропетровськ: РВВ ДНУ, 2010. – 138с.
5. “Structural Health Monitoring for Composite Materials” Jian Cai, Lei Qiu, Shenfang Yuan, Lihua Shi, PeiPei Liu and Dong Liang, In-Tech, 2012