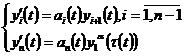 (1)
(1)Olinik A. S., Popova M. M., Vareh N. V., Аtаnоvа М. Y.
Oles Honchar Dnipropetrovsk National University
RESEARCH OF SOLUTIONS OF DIFFERENTIAL-FUNCTIONAL SYSTEMS WITH EVEN AND ODD AMOUNT OF EQUATIONS
In this paper we are making a research of differential equations systems with deviation of argument. Let us consider the system:
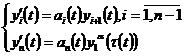 (1)
(1)
where 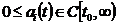 ,
, 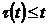 ,
, 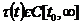
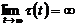 ,
, 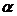 – odd numbers ratio, n=4,5.
– odd numbers ratio, n=4,5.
The system was examined when 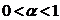 in [1]. In this paper the system is examined when
in [1]. In this paper the system is examined when 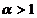 . Let’s give one of got results.
. Let’s give one of got results.
Theorem. Let the conditions be executed:
1) 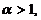
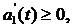
2) 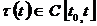 ,
, 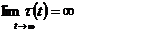
3) 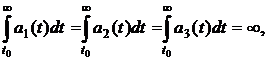
4) 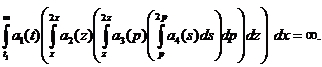
5) 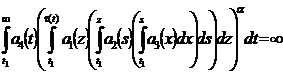
6) 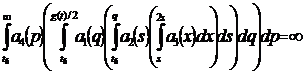
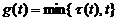
Then every solution of the system (1) either oscillates strongly, or each of its components tends to zero or to infinity when 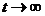 .
.
We also got the result for the system with odd amount of equations.
A similar result can be received in case, when argument deviation has a mixed nature.
The formulated result relates to the researches on the infinite interval.
The research of the differential systems was also made on finite interval.
Philips model of economic cycle is described as it’s shown below:
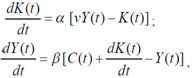
where 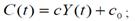
Y – profit, c – marginal propensity to the consumption, с0 – its component, which is independent from profit, K- stock; a, β, ν > 0 – parameters.
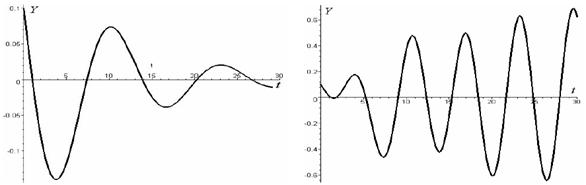
Fig. 1. Changing of revenue position temporally
These figures show deterioriation and growth of economy. The considered model of economic cycles is linear. The explicit solution was received and analysed due to this fact.
The described method allows us to find the differential equation solutions of the Philips economic cycle model depending on the final values of the certain input parameter.
The economic model that takes into account the aftereffect is built and explored on the base of this economic model.
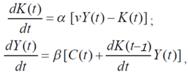
where: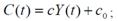
The model of capital and demand flow under the influence of profit standards in the developed market economy is explored with the odd number of equations.
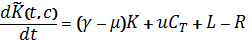 ;
; 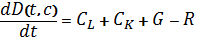
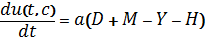 ;
;  ;
; 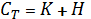 ;
; 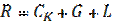
 is a distributing density of capital in the moment of t in space of technologies, that is capital value.
is a distributing density of capital in the moment of t in space of technologies, that is capital value.
D(t,c) – entrepreneurs, workers and government solvent demand on product which was produced according to the technology;
u(t,c) – is the profit standard distribution in the moment t in space of technologies.
On the basis of this model the new one is built. It takes into consideration solvent demand of entrepreneurs, workers and state, on produced product not only for today, but also for the past.