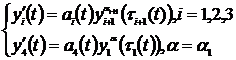
Derkachova V. V., Vareh N. V., Atanova M. Y.
Oles Honchar Dnipropetrovsk National University
RESEARCH OF THE SYSTEMS WITH THE EVEN AMOUNT OF DIFFERENTIAL EQUATIONS WITH DEVIATING ARGUMENT
This work deals with the research of the systems of differential equations with deviations of arguments with the even amount of equations.
Let us consider the following system:
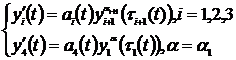
where αi – is relation of odd numbers,
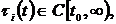
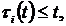
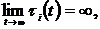
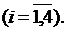
The results of research of solutions of the system (1) (τi (t) ≡ t, i=1, n-1), when αi = 1, i = 1,2,3; 0 < α <1 have been presented in the paper [1]. Unlike of that work the delays of arguments are included in every equation in this one. We'll adduce one of the got results.
Theorem 1. Let the conditions be executed: 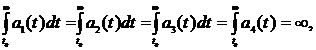 then every solution of the system (1) either oscillates strongly, or each its component tends to zero or to infinity at t→
then every solution of the system (1) either oscillates strongly, or each its component tends to zero or to infinity at t→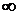 .
.
The condition 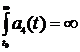 is very severe, that’s why we improved it with additional conditions
is very severe, that’s why we improved it with additional conditions 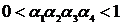 .
.
Theorem2. Let the conditions be executed:
1) 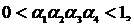
3) 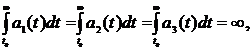 (2)
(2)
4) 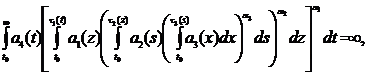 (3)
(3)
5)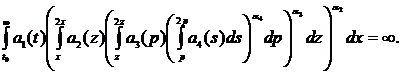 (4)
(4)
6)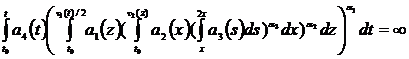 (5)
(5)
Then every solution of the system (1) either oscillates strongly, or each its component tends to zero or to infinity as t→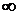 .
.
The formulated result relates to researches on finite interval.
The list of references:
1. Varekh N.V., Gorshkova P.G., Kukoyashna T.G., Marchenko A.V. “Research of differential equations with aftereffect”, “International Scientific Conference Mathematicalproblems of Technical Mechanics – 2011”, Dnepropetrovsk-Dneprodzerzhinsk, p.61.