
Burlay O. I., Kuznetsov K. A., Atanova M. Y.
Oles Honchar Dnipropetrovsk National University
INTELLIGENT SYSTEM FOR SUPPORTING DECISION-MAKING FOR DISPATCHING LIGHT OIL
Problem statement
"Dnepronefteprodukt" delivers light oil at gas stations by gasoline tankers. We need to make a decision about the importation of light oil products at some gas stations. We also need to find the shortest route f or oil tankers.
The designations
N – the total number of stations
F – the total number of fuel types
fq – the total cost of q-th fuel type 
ciq , diq – the volume and "dead" remains of the q-th tank on the i-th station 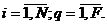
t0 – the current time
riq (t) –the remaining fuel in the q-th tank at the i-th station at time t.
wiq (t0±p) – the cumulative volume of the imported q-th fuel at the i-th station at time t0±p;
siq (t0±p) – the daily sales of the q-th fuel at the i-th station at time t0 ± p. t0±p.
There is a relationship:
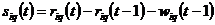 , (1)
, (1)
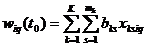
φiq – the time until the selling of fuel from the q-th tank from the i-th station stops.
 (2)
(2)
K – the total number of fuel trucks;
T – the cost of 1 km run of any fuel truck;
mk – the number of sections of the k-th fuel truck 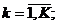
bsk – the volume of s-th section of the k-th fuel truck 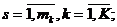
ρij – the distance in kilometers from the i-th to the j-th station 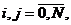 (0 – the index of the tank farm)
(0 – the index of the tank farm)
We should find the two sets of Boolean variables xksiq and ykij.
The mathematical model
Let us formulate the following restrictions:
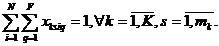 (3)
(3)
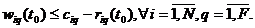 (4)
(4)
The variables are related by the following relation:
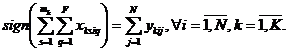 (5)
(5)
We also need to define a route that begins and ends at the oil tank.
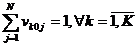 (6)
(6)
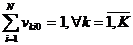 (7)
(7)
 (8)
(8)
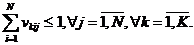 (9)
(9)
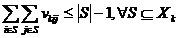 (10)
(10)
Where Xk – the set of the indexes of the stations, that are visited by k-th fuel truck
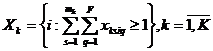 . (11)
. (11)
Optimality criterion
From a mathematical point of view, this problem is the task of the two- criterion optimization:
The first criterion is the integral criterion:
 . (13)
. (13)
And the second criterion:
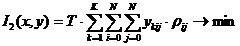 . (14)
. (14)
Solution to the problem
We created the graph of the routes to find the distances matrix (ρij). It was constructed on the basis of GIS OpenStreetMap ©. We also used the Floyd–Warshall algorithm for searching the shortest path. (APSP, All-pairs shortest paths). The complexity of the algorithm is Θ(n3), so we had to use nvidia graphics accelerator.
This is the statistical model:
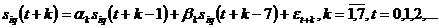 (15)
(15)
It consists of seven separated ARIMA-models (according to the 7 days of the week).
It demonstrates no more than 5% deviation from the observed data for more than 97% of the time series, and therefore it is acceptable for practical use.
The next model shows the dynamics of remaining fuel:
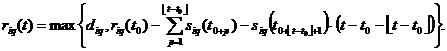 (16)
(16)
The examples given above allow us to calculate the criterion (14) value with all constraints (3)-(11) and (13) for any sets.
The dimension of the search space of our problem grows exponentially with the number of the stations. The use of random search leads to different solutions for the same input data. This is explained by the fact that each of these approaches has a probabilistic component.
Conclusion
The proposed optimization criteria are robust to changes in the input data. The successful experience of using the system shows that the current system may be applicable to a wide range of problems in transport logistics in Ukraine.