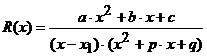К. т. н. Никулин А. В.

Днепродзержинский государственный технический университет, Украина

МЕТОД ЧАСТНЫХ ЗНАЧЕНИЙ ДЛЯ КОМПЛЕКСНЫХ КОРНЕЙ

Решение многих задач математического и комплексного анализа, теории дифференциальных уравнений и других разделов математики включает раз­ложение рациональных функций в сумму элементарных дробей и, возможно, полинома. Как известно [1; 2], после разложения на множители знаменателя дроби, представляющей рациональную функцию или ее часть, такая сумма определяется с точностью до значений постоянных коэффициентов в числи­телях элементарных дробей. Для нахождения неизвестных значений применяют метод неопределенных коэффициентов, а также метод частных значений. В результате переходят к решению линейной системы. Метод частных значе­ний имеет определенные преимущества для условий практических занятий со студентами по математике, так как приводит к решению разреженных ли­ней­ных систем и менее трудоемок. Однако в распространенных пособиях по мате­матике [1–3] реализация последнего метода рассматривается только в слу­чаях вещественных корней знаменателя.

Целью работы является распространение метода частных значений для упрощения выполнения выкладок на случаи комплексных корней, когда знаме­натели включают в качестве сомножителей квадратичные трехчлены с отрица­тельным дискриминантом. Как правило, по программе изучению разложения рациональных функций в сумму элементарных дробей предшествует изучение комплексных чисел и действий над ними, в том числе отделение вещественной и мнимой частей. В результате одно комплексное уравнение приводит к двум уравнениям с действительными величинами. Целесообразно использовать по­лу­ченные знания и приобретенные умения для последующего развития.

Для иллюстрации методики рассматривается типовой пример. Пусть необ­ходимо разложить рациональную функцию в виде правильной дроби

,

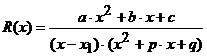где 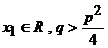 в сумму элементарных дробей. Переход совершается по фор­ муле

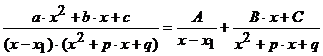
с заранее неизвестными коэффициентами А, В и С, которые находятся по мето­ду частных значений. После приведения правой части к общему знаменателю и приравнивания дробей получается тождество

.

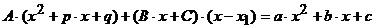Далее по методу частных значений:

при 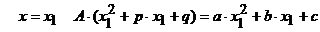, следовательно,

;

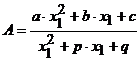при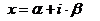 

.

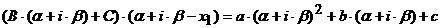После отделения вещественной и мнимой частей получается линейная система:

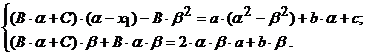
После решения системы определяются значения В и С.

Практическое значение имеют не получающиеся формулы, а алгоритм оп­ределения коэффициентов. Для оценки эффективности из [3] выбирается при­мер разложения:

Problem 9. Resolve 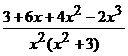 into partial fractions.

По предложенному алгоритму

.

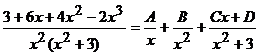В результате приведения правой части к общему знаменателю и прирав­нивания дробей получается тождество

.

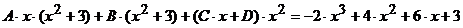По методу частных значений:

при

 ;

 ;

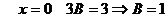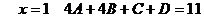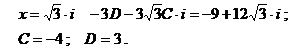
После решения второго уравнения определяется 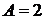. Затем после под­ста­новки найденных значений коэффициентов окончательно определяется раз­ложение на дроби

.

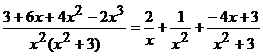По данным [3] с помощью метода неопределенных коэффициентов полу­чается такой же результат:

Hence, .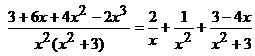

Эквивалентные разложения рациональных функций в суммы элементарных дробей

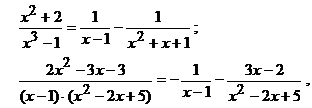
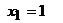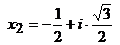полученные в [1; 2] методом неопределенных коэффициентов в случае ком­плексных корней знаменателя, находятся методом частных значений по пред­ложенной методике. В первом из рассматриваемых примеров используются корни знаменателя и , во втором – корни знаменателя 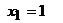и .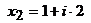

Рассматривается методика распространения метода частных значений при разложении рациональных функций в сумму элементарных дробей на случай комплексных корней знаменателя. Эффективность предложенного алгоритма проверена на типовых примерах распространенных пособий по высшей мате­матике. Получены эквивалентные результаты. На таком основании можно ре­комендовать использование метода частных значений на практических заня­тиях по высшей математике в случае вещественных и комплексных корней при решении задач интегрирования рациональных функций, нахождении ориги­налов преобразования Лапласа и т. д.

Список использованных источников:

1. Дубовик В. П. Вища математика: навч. посіб. / В. П.Дубовик, І. І. Юрик. – К.: А.С.К., 2003. – 648 с.

2. Письменный Д. Т. Конспект лекций по высшей математике: полный курс / Д. Т. Пись­менный. – 4-е изд. – М.: Айрис-пресс, 2006. – 608 с.

3. Bird J. O. Higher engineering mathematics / John Bird. – 5-th ed. – Oxford, Burligton MA: Newnes, 2006. – 726 p.