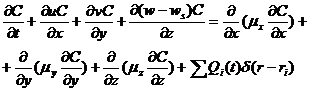Belyaeva V. V., Polishchuk O. A., Rusakova A. V.

Oles Honchar Dnipropetrovsk National University

MATHEMATICAL MODELING OF AIR POLLUTION EMISSIONS FROM SMALL BOILERS

Mini boilers are intense sources of air emission of various pollutants, and primarily, CO, soot, etc. So, the aggregate gross pollutant emissions, they take one of the first places among the other sources of emissions in the cities. In this regard, it is extremely important to forecast air pollution level while working in mini boilers [1].

The application of three-dimensional numerical model for the simulation of air pollution in mini boilers work is rather widespread in the cities. The model is based on equations of pollutant dispersion in the air [2; 3]:

,

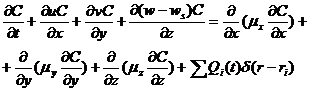where C – concentration of the pollutant in the atmosphere; u, v, w – velocity components of the air environment; 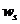  – the settling velocity of impurities; μ = (μx, μy, μz) – turbulent diffusion coefficient; Q – the intensity of the emission of pollutant;  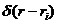 – delta Dirac function; ri = (xi,, yi,, zi) – coordinates of the source.

Calculation of the wind flow velocity field is based on the potential flow model. That is why, the model equation for the velocity potential P is the following:

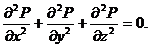
Numerical integration of the transport equation of the pollutant can be done with the help of the alternating triangular implicit difference splitting scheme [1]. Numerical integration of the equation for the velocity potential is done with the help of A. A. Samarskij’s method [4]. A specialized code is developed on the basis of created numerical model. This code helps to study the local air pollution in work of mini boilers. Its peculiarity is that it gives you a possibility to take into account the impact of buildings on the process of emissions dispersion in the atmosphere. Calculation of one task from this problem requires 10 seconds of computer time. The standard meteorological information is used for practical implementation of the developed model.

The list of references:

1. Zgurovsky M. Numerical modeling of environmental pollution environment / [M. Zgurovsky, V. Skopetsky, V. Khrushchev, N. Belyaev]. – K.: Science; Dumka, 1997. – 368.

2. Marchuk G. Mathematical modeling problem environment / G. Marchuk. – M.: Nauka, 1982. – 320.

3. Marchuk G. Methods of Computational Mathematics / G. Marchuk. – M.: Nauka, 1977. – 456.

4. Samara A. Theory of difference schemes / A. Samara. – M.: Nauka, 1983. – 616.