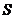– a roof of the carriage and height is 
; 
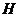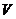– is the speed of the vertically falling raindrops. Thus 
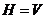because we mean only one second (Fig. 1). Dreus A. J., Siasieva A. A., Rusakova A. V.
Oles Honchar Dnipropetrovsk National University
WHEN RAIN CAN SOAK YOU STRONGER
One of the most interesting and important parts of mechanics is «Friction and resistance of medium». As an example, let us take a practical, simple, but rather instructive task: when will you soak your hat faster on the heavy rain – standing still for some period of time or moving? It would be easier to solve this task making a formula. The task: Rain falls vertically. When do the raindrops get the roof of a carriage – when this carriage is moving or when it is still?
Task solution: When the carriage stands still, the amount of raindrops getting its roof every second is equal to the amount of raindrops in a prism, a section is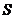
– a roof of the carriage and height is
;
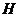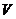– is the speed of the vertically falling raindrops. Thus
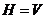because we mean only one second (Fig. 1).
More difficult is to take into account the amount of rain-water falling on the roof of moving carriage. Let us imagine the moving carriage and all total amount of falling raindrops that got such motion in relation to the ground, that is equal (on an absolute value) and opposite (in direction of) to the primary motion of the carriage. Then the carriage can be considered as unmovable in relation to the ground, and the raindrops will have a motion in relation to this unmovable carriage: vertically falling where the speed is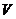
and horizontal movement forward to the carriage with speed 
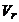. Resultant speed 
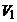will be inclined to the roof at some angle 
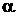. In other words, the carriage will be under the vertical rain (Fig. 2).
|
Fig. 1. Rain falling vertically on an immobile carriage |
Fig. 2. Case of locomotive carriage |
Now it is clear that amount of raindrops, which fall on the roof of moving carriage, is totally included in prism limits, where its section is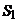 
perpendicular to rain direction but height 
is equal to the raindrops speed
(Fig. 3).
Fig. 3. Rain falling on the roof of locomotive carriage
Relation of areas of sections and heights of prism are equal respectively:
, 
.
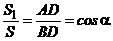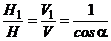The relation of the rain-water amount follows from here:
.
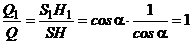Answer to the task: in both cases the amount of raindrops is absolutely equal. That’s why your hat will get wet the same in any case, whether you stand still under the rain for 30 minutes or run under the rain for the same time.
The list of references:
1. Перельман Я. И. Занимательная механика / Я. И. Перельман. – М.: Книговек, 2013. – 240 с.
