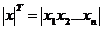 . Rating distribution law on the basis of series of orthonormal polynomials will be:
. Rating distribution law on the basis of series of orthonormal polynomials will be: Kuzmenko K. V., Lysenko N. A.,Timoshenko Zh. I.
Oles Honchar Dnipropetrovsk National University
ESTIMATING OF THE LAWS OF PROBABILITY DISTRIBUTIONS ON THE BASIS OF ORTHONORMAL POLYNOMIALS OF LAGUERRE
Most complete characteristic of statistics is the probability density function. The problem of estimating the probability density function has been studied for a long time, it was devoted a lot of work, but it remains relevant today [1]. This report examines one of the non-parametric methods, namely projection estimation [2; 3]. Projection methods are based on the decomposition of the desired density in a series of orthonormal system of functions.
Suppose that in the control sample are obtained measurements of random variables 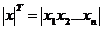 . Rating distribution law on the basis of series of orthonormal polynomials will be:
. Rating distribution law on the basis of series of orthonormal polynomials will be:
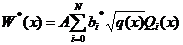 , (1)
, (1)
where 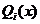 – the functions that make up an orthonormal system;
– the functions that make up an orthonormal system; 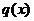 – weight function, and the coefficients
– weight function, and the coefficients 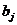 :
:
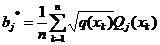 ;
;
normalizing factor 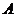 :
:
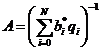 ,
, 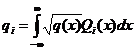 ;
;
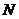 – the number of terms of the series, which is determined by the rule of «two zeros», described in [4]. From the structure of (1) follows that if the type of functions
– the number of terms of the series, which is determined by the rule of «two zeros», described in [4]. From the structure of (1) follows that if the type of functions 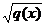 is similar to the distribution law
is similar to the distribution law 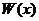 , we can expect that the number of terms
, we can expect that the number of terms 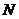 sufficient to effect recovery, will be small. Thus, the Laguerre polynomials
sufficient to effect recovery, will be small. Thus, the Laguerre polynomials 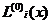 with weight function
with weight function 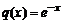 ,
, 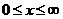 are recommended to restore asymmetric laws of probability distribution, similar to the exponential. Are Laguerre polynomials
are recommended to restore asymmetric laws of probability distribution, similar to the exponential. Are Laguerre polynomials  with weight function
with weight function 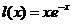 ,
, 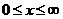 are used in the restoration of distribution laws with weak asymmetry.
are used in the restoration of distribution laws with weak asymmetry.
Difficulties in the practical application of this method of estimating the probability distribution of the laws are in a choose of type of weighting function with limited input data.
In this paper we investigated the error recovery laws of probability distribution series of orthonormal Laguerre polynomials of two types. In the computational experiment generated sampling distribution laws Rayleigh Weibull, Gamma and exponential distribution. Experimental samples of random variables with strong and weak asymmetry were restored by recovered two types of orthonormal Laguerre polynomials 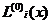 and
and  , error values obtained are summarized in the table. Practical recommendations about estimation of laws of distribution of probabilities by ranks of orthonormalized polynoms of Laguerre in the conditions of limitation of experimental data are offered.
, error values obtained are summarized in the table. Practical recommendations about estimation of laws of distribution of probabilities by ranks of orthonormalized polynoms of Laguerre in the conditions of limitation of experimental data are offered.
The list of references:
1. Крянев А. В. Математические методы обработки неопределенных данных / А. В. Крянев, Г. В. Лукин. – М.: Физматлит, 2003. – 216 с.
2. Суетин П. К. Классические ортогональные многочлены / П. К. Суетин – М.: Наука, 1976. – 328 с.
3. Ченцов Н. Н. Оценка неизвестной плотности распределения по наблюдениям / Н. Н. Ченцов // Доклады АН СССР. – 1962. – Т. 147, №1. – С. 45–48.
4. Малайчук В. П. Восстановление законов распределения вероятностей рядами ортонормированных полиномов / В. П. Малайчук, А. Н. Петренко, Н. А. Лысенко // Системні технології: рег. міжвуз. зб. наук. праць.–Дніпропетровськ: Системні технології. – 2005. – Вип. 3 (38). – С. 73–88.