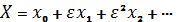Zelenskiy A. G., Pohasii N. E., Kriachunenko O. L.

Oles Honchar Dnipropetrovsk National University

APPLICATION OF PERTURBATION THEORY FOR SOLVING ALGEBRAIC AND TRIGONOMETRIC EQUATIONS AND SYSTEMS

What if the scientists didn’t see that Uranus’ orbit was the subject of gravitational perturbation by an unknown planet? What if we used the physics formulae in their authentic, exact shapes? In fact, we use their short, approximate forms nowadays. Maybe, in the former case, we could never see Neptune, because astronomers would have never found a new planet and astrophysics would have never calculated Neptune’s orbit. In the latter case, it would be very difficult to accomplish even the easiest physical calculation. In physics, we can find lots of examples of rounding in formulae and physic’s laws. We must know what data can be ignored and what must be obligatory used.

However, it’s not enough to define the problem. The solution of the task must be found as well as methods to solve the problem. In the other words, without some methods of perturbation scientists wouldn’t be able to solve many tasks. And examples mentioned above prove this statement.

Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly. Formally, we have for the approximation to the full solution X, a series in the small parameter, like the following: 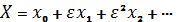 . Then we must substitute expansion into given equation and solve this equation.

My project consists of four parts. In the first part algebraic equations and methods of solving them were explored. Three types of equations were marked out: equation without repeated roots, equation with repeated roots and equations with small parameter at the highest term of equation. After solving the equations with a help of perturbation theory, obtained results were compared to the results gained by means of computer software. Relative errors were calculated and tabulated. As relative error appeared to be small, it is possible to conclude that perturbation theory is applicable for solving these types of equations and allows to obtain quite accurate results.

In the second part of research the perturbation theory was applied by the same method of expansion to the systems of algebraic equations. After solving a lot of systems it was defined that accuracy of results increases with decreasing small parameter and extending quantity of expansion terms. This fact was demonstrated on the example of one system and obtained results were tabulated into table of relative errors.

The third and the fourth chapters of the work are devoted to exploration of applying this theory for trigonometric equations and systems of equations. After calculations and analysis algorithm of perturbation theory application for trigonometric equations and systems was developed. In addition, the system of trigonometric equations with small parameter was solved.

Algorithm

1) Substitute 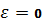  into given equation (system) and solve confluent equation (system).

2) Depending on the results of confluent equation (system) and position of small parameter choose the form of expansion.

3) Substitute expansion instead of variables into given equation (system).

4) Simplify the equation (system) considering the power of expansion.

5) Expand in Maclaurin series considering the power expansion (for trigonometric equation/system).

6) Group summands on the power of small parameter.

7) Solve (by analogy to a usual system of equation).

8) Substitute obtained results and find (evaluate) value of solutions of given equation (system).

Conclusions

As a general result the influence of small parameter on solution accuracy was explored. It was demonstrated and analyzed how quantity of small parameter influences on exactness of obtained results.

It was established that accuracy increases with decreasing small parameter and extending quantity of expansion terms.

There was completed analytic comparison of solutions obtained with perturbation theory and solutions obtained with computer programs/web-services. Close concordance of results was received.

Obtained solutions were verified and proved on the bases of constructed graphs of given equations and systems with a help of web-service Wolfram Alpha.

Therefore, we can conclude that advantage of perturbation theory as analytical method is that it makes possible to approximate solution without using specialized software and PC.

The list of references:

1. Найфэ А. «Введение в методы возмущений» / А. Найфэ. – М.: Мир, 1984.

2. Соболев В. А. «Метод возмущений: алгебраические уравнения» / В. А. Соболев. – 1999.

3. Гребенников Е. А. «Поиски и открытия планет» / Е. А. Гребенников, Ю. А. Рябов. – М., Наука, 1975.