Д. т. н., с. н. с. Мухамедиева Дилноз Тулкуновна
Центр разработки программных продуктов и аппаратно-программных комплексов, г. Ташкент, Республика Узбекистан
ПОДХОДЫ К РЕШЕНИЮ ЗАДАЧИ НЕЧЕТКОЙ ОПТИМИЗАЦИИ В ХЛОПКОВОДСТВЕ
Во многих задачах, встречающихся на практике, оказывается желательным учитывать влияние не одного, а многих параметров, от которых могут зависеть характеристики задачи. Действительно в большинстве случаев ограничения задачи линейного программирования представляет собой математическое описание и количественное выражение самых разнообразных условий, от которых зависит некоторый экономический, технический или производственный процесс. Эторазнообразие может сказаться, в частности, и в том, что причины, влияющие на изменение величин, при помощи которых выражаются соответствующие ограничения, необходимо рассматривать как независимые, но действующие одновременно. Задачи такого рода естественно описывать при помощи нескольких параметров [1; 2].
Параметрическую модель состава, соотношения угодий и их размещения на территории землепользования хлопчатника представим следующим образом.
Необходимо найти минимум себестоимости при установлении лимита капитальных вложений
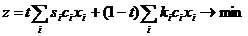
при обеспечении:
1) баланса земель
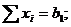
2) использования воды
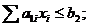
3) использования удобрений
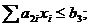
4) использования инвестиций
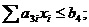
5) использования материальных ресурсов
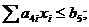
6) использования трудовых ресурсов
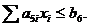
Приняты следующие обозначения:
x
i
– площади отдельных селекционных сортов хлопчатника (га); 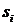 – себестоимость 1 ц хлопка-сырца (тыс. сум);
– себестоимость 1 ц хлопка-сырца (тыс. сум); 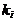 –капитальные вложения на 1 ц продукт (тыс. сум);
b
1 – общая площадь земель (га);
b
2 – ресурсы воды (м3);
a
1
i
– норма полива (м3/га);
a
2
i
– норма внесения удобрений (т/га);
b
3 – ресурсы удобрений (т);
a
3
i
– инвестиции на 1 га (тыс. сум);
b
4 – объем инвестиций (тыс. сум);
a
4
i
– норма материальных ресурсов (тыс. сум на1 га);
b
5 – ресурсы отдельных видов фондируемых материалов (тыс. сум).
–капитальные вложения на 1 ц продукт (тыс. сум);
b
1 – общая площадь земель (га);
b
2 – ресурсы воды (м3);
a
1
i
– норма полива (м3/га);
a
2
i
– норма внесения удобрений (т/га);
b
3 – ресурсы удобрений (т);
a
3
i
– инвестиции на 1 га (тыс. сум);
b
4 – объем инвестиций (тыс. сум);
a
4
i
– норма материальных ресурсов (тыс. сум на1 га);
b
5 – ресурсы отдельных видов фондируемых материалов (тыс. сум).
Часто имеется только «расплывчатая» – нечеткая информация о коэффициентах параметрической модели. Рассмотрим более внимательно параметры этой задачи 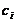 и
и 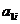 . Нетрудно понять, что величины этих параметров зависят от многих факторов реального процесса, не учтенных в приведенной здесь модели. Урожайность, например, зависит, и довольно сложным образом, от таких факторов, как наличие в почве тех или иных питательных веществ, сроков и технологии обработки почвы и внесения удобрений, солнечной активности и многих других. То же самое относится и к параметру
. Нетрудно понять, что величины этих параметров зависят от многих факторов реального процесса, не учтенных в приведенной здесь модели. Урожайность, например, зависит, и довольно сложным образом, от таких факторов, как наличие в почве тех или иных питательных веществ, сроков и технологии обработки почвы и внесения удобрений, солнечной активности и многих других. То же самое относится и к параметру 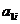 .
.
В качестве математического аппарата, позволяющего формализовать нечеткую априорную информацию, в статье применяется теория нечетких множеств. Задача параметрического программирования с S независимыми параметрами t 1, …, t s или S параметрическая задача в матричном виде записывается следующим образом:


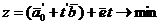

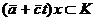 (1)
(1)
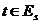 ,
,
где
K
={y 
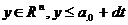 } – заданное выпуклое подмножества пространства
Rn
.
} – заданное выпуклое подмножества пространства
Rn
.
Задачу такого типа можно назвать задачей параметрического программирования с множественно-значными коэффициентами. Ясно, что в рамках этой задачи не имеет смысла говорить о максимизации функции цели, поскольку значения этой функции – не числа, а множество чисел. В этом случае необходимо выяснить, какое отношение предпочтения в множестве альтернатив порождает эта функция, а затем исследовать вопрос о том, какие выборы считать рациональными в смысле этого отношения предпочтения.
Следующим шагом на пути уточнения рассматриваемой модели является описание коэффициентов задачи в форме нечетких множеств. При этом, кроме задания множеств возможных значений параметров, в модель вводится дополнительная информация в виде функций принадлежности этих нечетких множеств. Эти функции можно рассматривать как способ приближенного отражения экспертом в агрегированном виде имеющегося у него неформализованного представления о реальной величине данного коэффициента.
Итак мы пришли к постановке задачи нечеткого параметрического программирования.
Задача (1) сводится к следующей задаче параметрического программирования 
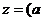
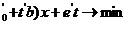

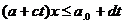 (2)
(2)
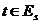 ,
,
в которой значения коэффициентов
a
,
b
,
c
,
d
,
e
описаны в форме нечетких подмножеств, т. е. заданы функции принадлежности 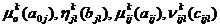 и
и 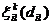 cоответствующих множеств, где
i
= 1, …,
m
;
j
= 1, …,
n
;
l
= 1, …,
s
и
cоответствующих множеств, где
i
= 1, …,
m
;
j
= 1, …,
n
;
l
= 1, …,
s
и
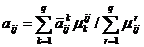 ,
, 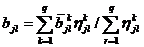 ,
,
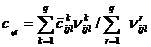 ,
, 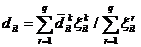 .
.
Решением задачи (2) называется явным образом заданная решающая функция
zs
(
t
)=min 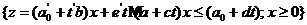 .
.
Разработан алгоритм и составлена программа по этой методике [3].
Список использованных источников:
1. Орловский С. А. Проблемы принятия решений при нечеткой исходной информации / С. А. Орловский. – М.: Наука, 1981.
2. Подиновский В. В. Парето – оптимальные решения многокритериальных задач / В. В. Подиновский, В. Д. Ногин. – М.: Наука, 1982.
3. Мухамедиева Д. Т. Разработка нечетких моделей задач прогнозирования и оптимизации / Д. Т. Мухамедиева. – Ташкент: изд-во «Фан ва технология», 2012. – 346 с.