Федорова Олександра Петрівна, к. т. н., доц. Нецветаєв Володимир Анатолійович

Національний гірничий університет, м. Дніпропетровськ, Україна

ОПТИМІЗАЦІЙНА МОДЕЛЬ ОТРИМАННЯ ПРИБУТКУ З УРАХУВАННЯМ ФУНКЦІЇ ПОПИТУ

Модель отримання прибутку від випуску одного виду продукції на промисловому підприємстві описується наступними алгебраїчними рівняннями:

;

;

;

;

,

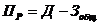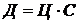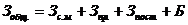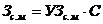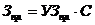де Пр  – прибуток, грн;  Д  – дохід (вхідний грошовий потік), грн;  Ц  – ціна продажу продукції, грн;  С  – попит (кількість);  Зобщ .  – загальні витрати;  Зс.м .  – витрати на сировину та матеріали, грн;  Зпр .  – витрати на виробництво, грн;  Зпост .  – постійні витрати;  Б  – брак, відходи, некондиція и т. д.;  УЗс.м .  – питомі витрати на сировину та матеріали, що поставляються на виробництво одиниці товару;  УЗпр .  – питомі витрати на виробництво одиниці товару.

Для побудови моделі необхідно мати такі вихідні дані, представлені таблично у вигляді часових рядів: питомі витрати на виробництво; постійні витрати; брак, відходи, некондиція; питомі витрати на сировину і матеріали; попит чи обсяг продажу. За даними цих таблиць будуються прогнозні моделі на наступний період. В основу побудови оптимізаційної моделі покладена формула, прибутку:

,

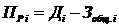де   i  – номер місяця,  Дi  – функція доходу (величина, яка змінюється в часі), Зобщ  i  – функція загальних витрат (величина, яка змінюється в часі).

Функція доходу буде виглядати так:

,

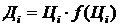де 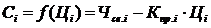 – у простійшому випадку лінійна, а у загальному випадку нелінійна функція попиту, яка відображає залежність попиту  Сі  від ціни  Ці  у різні інтервали часу.  Чсв  і  – вільний член лінійної функції попиту,  Кпр  і  – коєффіціент пропорційності у функції попиту.

З урахуванням функції попиту, рівняння доходу:

.

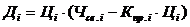Функцію загальних витрат знайдемо, грунтуючись на формулах отримання прибутку:

,

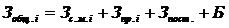де   ,  .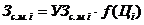

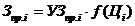Після підстановки і перетворення, отримаємо:

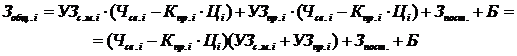
Функція прибутку (максимізована функція оптимізаційної задачі) матиме вигляд:

.

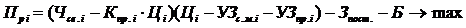Ця функція є цільовою, обмеження якої складаються з конкретних кількісних значень змінних моделі. Система обмежень буде мати наступний вигляд:

,

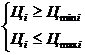де Цmin  =  Цсебест .  – собівартість продукціі;  Ц max = Црын .  – ринкові ціни на продукцію.

У систему обмежень, крім нерівностей, входять також наступні рівності:

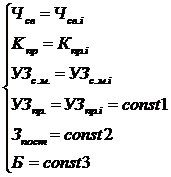
Значення вільного члена, коефіцієнта пропорційності і питомих витрат на придбання сировини та матеріалів щомісяця змінюються, а величина браку, питомих витрат на виробництво одиниці продукції і постійних витрат планується керівництвом не змінювати протягом року.

При вирішенні оптимізаційної задачі знаходиться максимальний прибуток за місяць, щоб знайти максимальний прибуток за квартал, формула буде мати наступний вигляд:

,

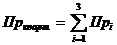а за рік:

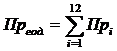
Рішення оптимізаційної задачі виконується за допомогою надбудови «Пошук рішення» табличного процесора Excel для кожного прогнозованого місяця, кварталу, року, причому прибуток за рахунок оптимізації у всіх випадках збільшується за рахунок вибору оптимальної ціни, яка є змінною рішення.

Список використаних джерел:

1. Экономическое моделирование в Microsoft Excel / Джефри Мур, Лари Р. Уэдерфорд и др. – 6-е изд.; пер. с англ. – М.: Вильямс, 2004. – 1024 с.: ил.