К. е. н., доц. Краснюк Максим Тарасович

Київський національний економічний університет імені В. Гетьмана самоврядний (автономний) дослідницький ВНЗ

ЗБІЛЬШЕННЯ КАПІТАЛІЗАЦІЇ ТА РЕСУРСНОЇ БАЗИ ВІТЧИЗНЯНИХ НАФТОГАЗОВИХ КОМПАНІЙ ЧЕРЕЗ ЗАСТОСУВАННЯ ГІБРИДНИХ ТЕХНОЛОГІЙ ІНТЕЛЕКТУАЛЬНОГО АНАЛІЗУ КОРПОРАТИВНИХ ДАНИХ

Збільшення ресурсної бази вітчизняних нафтогазових компанії наразі стає все більш актуальним завданням для національної економіки.

На стагнацію обсягів видобутку впливають специфічні локальні особливості видобутку вуглеводнів в Україні (для свердловин характерні малий дебіт,обводненість, відкладення піщаних і сольових пробок на вибоях; вплив на продуктивність тиску у системах збору, транспорту газу, необхідність 2-х ступеневогокомпресування газу для подачі споживачам; врахування специфіки кожного родовища (різний конденсатний фактор, наявність сірководню і вуглекислого газу та інше)).

Ситуація ускладнюється і тим, що при постійному погіршенні структури запасів на старих родовищах, щорічне введення в експлуатацію нових, невеликих за запасами родовищ, не може компенсувати природне падіння видобутку на старих родовищах. Світова практика засвідчує, що великі родовища забезпечують 60–80 % всього видобутку.

Враховуючи вищенаведене, та зважаючи на те, що ступінь вивченості нафтогазоносних басейнів України надзвичайно високий – виявлення значних зазапасами нових та економічно-обгрунтованих покладів вуглеводнів в цих умовах із затосуванням класичних підходів – надзвичайно складне завдання.

Нетрадиційні поклади нафти і газу вважаються одним з найперспективніших напрямків розвитку мінерально-сировинної бази. Для такого типу покладів не працюють стандартні методи виділення колектора й оцінки його параметрів.

Тому актуальним є застосування гібридних методів інтелектуального аналізу накопичених компаніями геолого-геофізичних та геолого-економічних даних з метою ідентифікації на попередньо-досліджених потенційних площах (родовищах) нетрадиційних (аномальних) покладів вуглеводнів.

Інтелектуальний аналіз даних у умовах глобалізації є одним з механізмів підвищення ефективності та глобальної конкурентноздатності підприємств.

Саме задача пошуку аномалій в накопичених даних наразі є провідною серед використовуємих паттернів інтелектуального аналізу даних з погляду на швидкість отримання результатів та їх економічний ефект.

Для вирішення поставленої задачі автором запропоновано та апробовано наступні два алгоритми стійкої кластеризації накопичених компаніями геофізичних даних: модернізований алгоритм CFF та модернізований алгоритм k-середніх.

Модернізований алгоритм кластеризації CFF – алгоритм, створений для вирішення проблеми кластеризації зашумлених даних (наявність природних та/або штучних завад при реестрації даних геофізичних досліджень свердловин) і визначення в процесі кластеризації невідомого заздалегідь числа кластерів складної форми. Алгоритм складається із двох частин.

1.  Виконується вибір підмножини даних, розташованих у областях з високою щільністю точок шляхом оцінки щільності розподілу в кожній із точокз використанням ядерних непараметричних оцінок щільності;

2. Виконується безпосередньо процес кластеризації шляхом побудови графа, вершинами якого є відібрані на першому кроці точки X1, причому, точки Xt і Xjз’єднані разом тільки якщо евклідова відстань між ними не перевищує граничного значення ɛ.

У ситуації, коли важливо оцінити якість кластеризації (зокрема при прийнятті рішень про інвестування у розробку виявленого продуктивного покладу) та наявністю кластерів складної форми, саме модернізований алгоритм k-середніх дозволяє виконати кластеризацію на оптимальну кількість кластерів. Таким чином, алгоритм вирішує два завдання. Перша – визначення найбільш імовірної кількості кластерів (у заданому діапазоні). Друга – одержання більш стійкого результатукластеризації, тому що багаторазове повторення знижує вплив випадкового розподілу початкових центрів.

Алгоритм складається із двох кроків

1. Обчислюється найбільш імовірна (у частотнім відношенні) кількість кластерів за допомогою модифікації алгоритму k-середніх.

2. Проводиться процес багаторазового повторення кластеризації по алгоритму k-середніх для одержання стійкого результату розбивки вихідної множини об’єктів на оптимальне число кластерів шляхом оцінки ймовірності розподілу. Після завершення процесу для кожного спостереження обчислюється найбільш імовірний кластер, тобто кластер, у який дане спостереження було віднесено найбільше число раз. Таким чином, у результаті виходить не тільки поділ на кластери, але й характеристика кластеризації – імовірність віднесення кожного об’єкта (спостереження) до свого кластера. Поряд з візуалізацією поділу на кластери може бути представлена візуалізація ймовірностей віднесення до кластерів.

Важливо помітити, що вкрай бажано передбачити в процедурі кластеризації імовірнісний елемент, тобто вказати довірчі ймовірності й довірчі інтервали для числа кластерів залежно від числа ознак (атрибутів).

Існує множина індексів кількісної оцінки якості кластеризації, наприклад, індекси Bezdek, Dunn, Xie-Beni, Davies-Bouldin, Gath-Geva. Більшість цих індексів звичайно неявно допускають, що точки даних мають постійну щільність у кластерах. Однак, це не притаманно предметній області даного дослідження.

Тому, поряд з розробкою математичного апарата кластеризації, важливе значення мають засоби представлення результатів кластерного аналізу й оцінки вірогідності цих результатів.

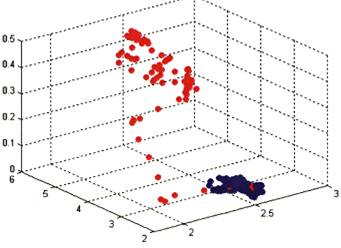
Запропоновані підходи до тривимірної візуалізації показують, що аномальні по пористості об’єкти, які й уміщають породи (граніти) розділяються (принаймні, частково) у тривимірному просторі. На рис. 1 представлений тривимірний кросплот, на осях відзначені наступні параметри: ФЕП, щільність, пористість (синім кольором виділена вміщаюча порода, червоним – аномальний об’єкт).

Рис. 1. Тривимірна візуалізація аномального інтервалу

(синім кольором виділена вміщуюча порода, червоним – аномальний об’єкт)

Така 3D візуалізація наводить на думку, що можна використовувати математичний апарат кластеризації для коректного розмежування цих об’єктів.

Наступним кроком є вирішення завдання знайти поверхню, яка розмежовує об’єкти в багатомірному просторі.

Математично завдання поділу двох множин точок у просторі трьох і більшого числа вимірів можна виконати декількома способами: застосування методології розпізнавання образів або затосуванням дискримінантної поверхні.

Перший варіант полягає в застосуванні ідеології розпізнавання об’єктів. Рішення завдання розпізнавання образів – визначення приналежності об’єкта або їх набору до однієї із заданих груп. У геометричній інтерпретації під групою (образом) розуміється область в 3-х вимірному просторі, уздовж координатних осей якого відкладені значення ознак. Об’єкт – точка в 3-х вимірному просторі. Еталонний об’єкт – це точка, про яку заздалегідь відомо до якої групи вона належить. Враховуючи зроблені визначення, завдання розпізнавання образів можна розуміти як зіставлення деякого об’єкта, щодо якого невідомо, до якої групи він відноситься, з еталонними. У цьому випадку об’єкт зрівнюється з еталонними об’єктами кожної групи й відноситься до тієї або іншій групи на основі заздалегідь обраного критерію відповідності або подоби.

Ідея другого методу – застосування дискримінуючої поверхні – полягає в побудові поверхні (площини, симплексу), відображувані об’єкти на типи (рис. 2). В задачі аналізу та інтерпретації даних геофізики свердловин така площина повинна бути побудована, таким чином, щоб нижче її перебували б пласти з водоносних інтервалів, а вище – нафтогазоносних. Інують різні метрики, які ми прагли б використовувати для коректного вирішення геофізичного завдання розмежування пластів: Центроїдна відстань, Медіанна відстань, Відстань, що обчислюється за принципом «далекого сусіда», Середнє арифметичне відстаней, обчислених за принципом «далекого сусіда» і за принципом «найближчого сусіда», Відстань, що обчислюється між «центром ваги» однієї множини й найбільш віддаленою від нього точкою іншої множини, Відстань, що обчислюється між «центром ваги» однієї множини й найближчої до нього точкою іншої множини. З огляду на результати тестів, випливає, що деякі метрики для вирішення поставленої задачі аналізу є неефективними (наприклад, відстань, що обчислюється за принципом далекого сусіда, або максимальна відстань). Результати доліджень показали, що застосування наступних метрик для аналізу даних геофізики свердловин є результативним: відстань між центрами ваги двох об’єктів або медіанна відстань.

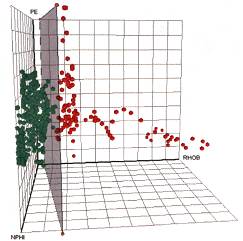
Рис. 2. Візуалізація аномального інтервалу свердловини

Важливо зауважити, що усі побудови передбачають однорідність од. виміру величин по осях. Однак реально всі величини є геофізичними параметрами й мають різну роздільну здатність. Отже, математично точна побудова вимагає спочатку приведення всіх геофізичних параметрів до безрозмірного виду (наприклад, нормувати на максимальну величину), а потім введення міри (наприклад, евклідової). Ця процедура є математично вірною, але отримана побудова майже повністю втрачає геофізичну наочність та непридатна для подальшої інтерпретації.

Список використаних джерел:

1. Геолого-методичні принципи оцінювання запасів (ресурсів) вуглеводнів у надрах / [М. І. Євдощук, С. П. Євдощук, О. Й. Пінчук, В. Я. Сініцин] // Нафтова і газова промисловість. – 2001. – № 1. – С. 11–14.

2. Карамишев О. С. Значення геолого-економічної оцінки геологорозвідувальних робіт в ринкових умовах надрокористування / О. С. Карамишев, В. А.  Романюк // Нафтова і газова промисловість. – 1998. – № 6. – С. 3–5.

3. Краснюк М. Т. Нечіткі орієнтовані на знання засоби підтримки прийняття інвестиційних рішень нафтогазовидобувної компанії / М. Т. Краснюк // Економіка та підприємництво: зб. наук. праць молодих учених та аспірантів. – Вип. 9; відп. ред. С. І. Дем’яненко. – К.: КНЕУ, 2002. – 200 с.

4. Краснюк М. Т. Технології штучного інтелекту та гібридний підхід в орієнтованих на знання СППР (на прикладі нафтогазовидобувної компанії) / М. Т. Краснюк // Моделювання та інформаційні системи в економіці: Міжвідом. наук. зб.; відп. ред. М. Г. Твердохліб. – К.: КНЕУ, 2002. – Вип. 68. – 190 с.

5. Краснюк М. Т. Особливості розвитку геолого-економічних інформаційних технологій у галузі розвідки і розробки нафтогазових родовищ на Україні / М. Т. Краснюк, О. І. Гафич // Моделювання та інформаційні системи в економіці. – К.: КНЕУ, 2006. – № 74. – С. 182–192.

6. Краснюк М. Т. Управління економічним ризиком інвестування у газовидобувну галузь / М. Т. Краснюк // Зб. наук. пр. за мат. Першої Всеукр. наук.-практ. конф. «Проблеми економічного ризику: аналіз та управління». – К.: КНЕУ, 1998. – С. 36–37.

7. Краснюк М. Т. Розробка ефективної методики геолого-економічного моделювання і оцінки ризиків нафтогазовидобувних проектів / М. Т. Краснюк, О. І. Гафич // Моделювання та інформаційні системи в економіці. – К.: КНЕУ, 2007. – № 75.

8. Краснюк М. Т. Систематизація, моделювання та оцінка галузевих ризиків при техніко- та геолого-економічному обґрунтуванні інвестиційних проектів нафтогазовидобутку / М. Т. Краснюк, О. І.Гафич // Моделювання та інформаційні системи в економіці. – К.: КНЕУ, 2007. – № 76. – С. 95–106.

9. Краснюк М. Т. Моделювання ризику участі компанії-інвестора в проектах пошуку і розвідки нафти і газу / М. Т. Краснюк, О. І. Гафич // Економічний вісник Національного гірничого університету. – 2010. – № 1. – C. 102–111.

10. Нафта і газ України / під ред. М. П. Ковалко та ін. – К.: Наукова думка, 1997. – 380 с.

11. Юрчишин В. М. Економіко-екологічні аспекти інформаційного моделювання нафтогазових об’єктів / В. М. Юрчишин // Нафтова і газова промисловість. – 2001. – № 4. – С. 54–56.