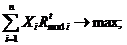
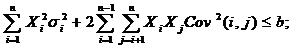
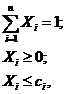
К. т. н., доц. Нецветаєв Володимир Анатолійович, Мусієнко Анастасія Юріївна
Національний гірничий університет, м. Дніпропетровськ, Україна
УТОЧНЕНІ ОПТИМАЛЬНІ ІНВЕСТИЦІЙНІ ПОРТФЕЛІ
Істотний внесок до математичної теорії і практики інвестиційних портфелів внесли відомі вчені Джеймс Тобін, Гарі Марковіц, Мертон Міллер, Уїльям Шарп та ін. [1]. Ця робота ставить за мету уточнення формул оптимальних інвестиційних портфелів з урахуванням часових прогнозних моделей показників прибутковості активів.
Формалізований опис уточненого портфеля максимальної прибутковості прийме наступний вигляд:
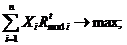
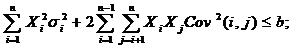
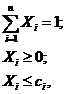
де
i
– номер цінного паперу в інвестиційному портфелі (i=1.n); 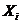 – частка цінних паперів
i
в інвестиційному портфелі;
– частка цінних паперів
i
в інвестиційному портфелі; 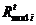 – прибутковість цінних паперів
i
в
t
момент часу (t=1.m);
– прибутковість цінних паперів
i
в
t
момент часу (t=1.m); 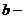 верхня межа ризику;
верхня межа ризику; 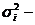 дисперсія доходів цінних паперів
дисперсія доходів цінних паперів 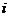 за період m років;
за період m років; 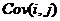 – коваріація доходів цінних паперів за період
m
років;
– коваріація доходів цінних паперів за період
m
років;
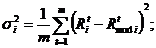
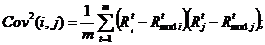
Формалізований опис скоректованого оптимального інвестиційного портфеля мінімального ризику матиме наступний вигляд:
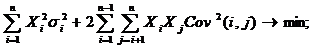
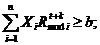
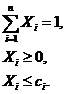
де
i
– номер цінного паперу в інвестиційному портфелі (i=1.n); 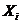 – частка цінних паперів
– частка цінних паперів 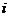 в інвестиційному портфелі.
в інвестиційному портфелі. 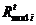 – прибутковість цінних паперів
i
в
t
момент часу (t=1.m);
b
– нижня межа очікуваного річного доходу від всіх інвестицій;
– прибутковість цінних паперів
i
в
t
момент часу (t=1.m);
b
– нижня межа очікуваного річного доходу від всіх інвестицій; 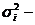 дисперсія доходів цінних паперів
дисперсія доходів цінних паперів 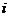 за період
m
років;
за період
m
років; 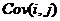 – ковариаціядоходів цінних паперів за період
m
років
– ковариаціядоходів цінних паперів за період
m
років
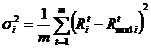 ;
; 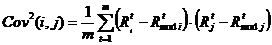
У запропонованій оптимізаційній моделі мінімального ризику, як і для уточненої моделі максимальної прибутковості, спочатку пропонується побудувати прогнозні моделі зміни прибутковості всіх пакетів акцій за минулий проміжок часу. Для цього може використовуватися один з відомих методів прогнозування. Потім слід набути всіх значень прогнозної моделі, після чого, підставити їх у вирази для розрахунку дисперсій і коваріацій, зпрогнозовані на k = 1,2.l крапок вперед значення доходностей цінних паперів – у вираз для обмеження оптимального портфеля. По суті, для обох портфелів мова йде не про зміну методики оптимізації, а про підвищення точності розрахунку оптимального портфеля максимального прибутку або мінімального ризику, за рахунок застосування точнішої моделі при розрахунку прибутковості, що, проте, вносить свої корективи і у формули оптимального портфеля. За допомогою скоректованої моделі можна отримувати параметри з тією ж нижньою межею прибутковості, але з меншим, в порівнянні з відомою моделлю, значенням ризику, що є вельми важливим для практики. Крім того, оптимальний портфель можна розраховувати на k = 1,2.l кроків вперед, і для кожного прогнозного інтервалу він буде різним, що також важливо для виконання поточної корекції інвестиційного портфеля [2].
Оптимальний портфель може бути представлений у матричному вигляді, якщо ввести в розгляд прямокутну ковариаційну матрицю COV , одновимірний масив часток X , і одновимірний масив P , рівний їх добутку
P = X COV .
У розгорнутому вигляді цей вираз може бути записано таким чином:
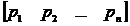 =
= 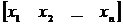
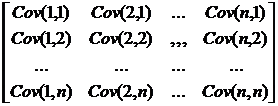
Зауважимо, що діагональні елементи прямокутної ковариационной матриці являють собою дисперсії. З урахуванням вищевикладеного, формалізоване подання портфеля мінімального ризику цінних паперів буде мати наступний компактний вигляд:
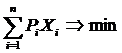 ;
; 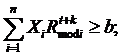
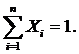
Різниця між початковою моделлю та удосконаленою полягає в формулах розрахунку прибутковості кредитів та коваріацій.
Оптимальний портфель максимальної прибутковості матиме аналогічний вигляд при заміні цільової функції на обмеження, а обмеження – на цільову функцію.
Список використаних джерел:
1. Экономическое моделирование в Microsoft Excel / [Мур, Джеффри, Уэдерфорд, Ларри Р. и др.]. – 6-е изд.: пер. с англ. – М.: Вильямс, 2004. – 1024 с.: ил.
2. Нецветаєв В. А. Оптимальне управління інвестиційними портфелями з урахуванням тенденцій зміни прибутковості / В. А. Нецветаєв // Економічний вісник Національного гірничого університету. – 2010. – № 2. – С. 121–129.