WEB-ресурс научно-практических конференций

Чернова Л.С.

Национальный университет кораблестроения имени адмиралаС.О.Макарова, г . Николаев, Украина

МОДИФИКАЦИЯ ЗАДАЧИ О РАНЦЕ И ЕЕ РЕШЕНИЕ ПРИМЕНИТЕЛЬНО К УПРАВЛЕНИЮ СТОИМОСТЬЮ ПРОЕКТА, ОСНОВАННОМУ НА КОМПЛЕКСНОМ ИСПОЛЬЗОВАНИИ ФУНКЦИОНАЛЬНО-СТОИМОСТНОГО АНАЛИЗА И БЮДЖЕТИРОВАНИЯ

Задача о ранце (рюкзаке) – одна из задач комбинаторной оптимизации , которая получила название от максимизационной задачи укладки как можно большего числа нужных вещей в рюкзак при условии, что общий объём (или вес) всех предметов, способных поместиться в рюкзак, ограничен[1]. Подобная задача широко распространена в экономике, градостроительстве, прикладной математике, криптографии и других областях деятельности человека. В общем виде, задачу можно сформулировать так: из неограниченного множества предметов со свойствами «стоимость» и «вес», требуется отобрать некое число предметов таким образом, чтобы получить максимальную суммарную стоимость при одновременном соблюдении ограничения на суммарный вес. Применительно к экономике хочется привести пример известной экономической задачи. Бутлегеры во времена сухого закона в США планируют поставки алкогольной продукции. 5 крупных городов готовы платить за тонну спиртного: 2000 $ в Бостоне, 3000 _ $ в Детройте, 2500 $ в Вашингтоне, 3200 $ в Нью-Йорке и 1800 $ в Чикаго. Все 5 городов находятся на разном расстоянии от порта, куда прибывает груз: Бостон – 250 миль , Детройт – 300 миль , Вашингтон – 500 миль , Нью-Йорк -100 миль и Чикаго – 600 миль . Требуется выбрать города, в которых можно получить максимальную прибыль от продажи спиртного. При этом суммарное расстояние от этих городов до порта с грузом не должно превышать 1000 миль .

Теперь попробуем сформулировать эту задачу применительно к теме этой статьи. Предприятие хочет реализовать проект создания нового двигателя, при этом предприятию необходимо получить при минимальных затратах максимальную прибыль, т. е. заполнить ранец необходимыми предметами с минимальным весом, обладающими при этом максимальной стоимостью. Очевидно, что под минимальным весом предметов следует понимать оптимизированные с помощью функционально-стоимостного анализа бюджеты бизнес-процессов проекта создания нового двигателя, а под максимальной стоимостью – ожидаемую прибыль от реализации новых двигателей. Объем ранца – это, соответственно, размер собственных средств и средств инвесторов.

Целью настоящей статьи является описание методики применения функционально-стоимостного анализа при управлении процессом бюджетирования бизнес-процессов при реализации проекта создания нового двигателя наукоемким предприятием ГП НПКГ «Зоря – « Машпроект » [2].

Управление стоимостью проекта включает в себя:

· оценку стоимости проекта;

· бюджетирование проекта – установление целевых показателей затрат на реализацию проекта по каждому бизнес-процессу;

· контроль стоимости проекта.

Практика показала, что целесообразно выделять на предприятии пять видов бизнес-процессов, а именно:

· основные бизнес-процессы по производству продукции и предоставлению услуг;

· вспомогательные бизнес-процессы, обеспечивающие основные;

· бизнес-процессы развития предприятия;

· бизнес-процессы управления деятельностью предприятия;

· бизнес-процессы, обеспечивающие управление конкретным проектом.

Каждая составляющая накладных расходов проекта порождается определенной функцией, принадлежащей какому-либо бизнес-процессу. Каждый бюджет должен учитывать некоторую долю накладных расходов пропорционально той функции, которая финансируется из соответствующего бюджета. Итак, решим задачу, связанную с определением оптимальных бюджетов бизнес-функций проекта создание нового двигателя с использованием метода функционально-стоимостного анализа.

Имеется n бюджетов центров финансовой ответственности реализуемого проекта. Обозначим через y _i объем финансирования i -го бюджета. Эффективность разработанного бюджета определяется выражением:

D _i ( y _i ) = _i max [0; y _{i –} a _i ], i = ,

где a _i – постоянные затраты в i -м бюджете;

_i – эффективность i -го бюджета, определяемая путем сравнения фактического i -го бюджета и его параметров, полученных методом функционально-стоимостного анализа с учетом ранга функции бизнес-процесса.

Заданы ограничения y _i ? С _i , i = , где С _i – максимальный предельный объем финансирования i -го бюджета, определяемый возможностями предприятия и рыночным спросом. Задана также величина инновационного фонда R .

Определим множество бюджетов проекта и объем финансирования каждого бюджета с учетом его эффективности, определяемой методом функционально-стоимостного анализа, так, чтобы суммарный доход был максимальным при ограничении на суммарную величину инновационного фонда. Задача заключается в максимизации

D ( y )= S D _i ( y _i ) ,

при ограничениях

0 ? y _i ? C _i .

Для решения задачи применим метод дихотомического программирования. Сначала докажем простую теорему, позволяющую уменьшить объем вычислений.

Теорема. Существует оптимальное решение, такое, что все принятые к разработке бюджеты (за возможным исключением одного бюджета) финансируются в максимальном объеме.

Следствие. В множестве принятых к разработке бюджетов финансирование менее максимального может иметь бюджет с минимальной эффективностью.

Рассмотрим структуру дихотомического представления в виде ветки дерева, вершины которого расположены в порядке нумерации бюджетов. В этом случае метод дихотомического программирования переходит в метод динамического программирования. Обозначим F ( k ; p ) – максимальный эффект от первых k бюджетов при величине инвестиционного фонда P . Уравнение Беллмана имеет вид

F ( k+l ;p ) = [F ( k;p -q);d _k+1 max [0;q-a _kH ]]

Рассмотрим другой алгоритм решения задачи, также использующий теорему 1. А именно, поскольку только один бюджет может быть разработан с финансированием менее максимального , то рассмотрим n задач.

В i - й задаче принимается, что бюджет i может быть разработан с финансированием менее максимального . Исключая этот бюджет, мы получаем классическую задачу о ранце. Для оставшихся бюджетов, как известно, решение задачи о ранце дает одновременно и оптимальное решение для всех меньших величин i . Обозначим Ф _i ( p ) – максимальный эффект в i – й задаче в зависимости от финансирования p . Максимальный эффект с учетом бюджета i определяется выражением

Сравнивая решения n задач, определяем оптимальное решение. Таким образом, необходимо решить n задач о ранце. Однако применение метода дихотомического программирования позволяет существенно уменьшить это число. Действительно, если например, решена задача о ранце для первых ( n – 1 ) бюджетов, то для решения задачи без бюджета ( n – 1 ) достаточно взять решение для первых ( n – 2 ) бюджетов и решить только одну задачу, добавив бюджет n . Соответствующая структура дихотомического представления для n задач о ранце приведена на рисунке 1 (для случая n = 5 ).

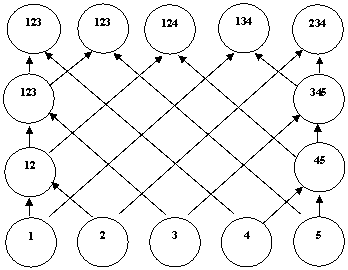
Рис. 1. Структура дихотомического представления для 5 задач о ранце

Поясним эту структуру. Сначала решаются задачи о ранце без бюджета 5 и 1 (левая и правая ветки на рисунке 1). Для получения решения задачи без бюджета 4 решаем всего одну задачу для объединенных бюджетов 1, 2, 3 и бюджета 5. Всего решается 3( n – 2) подзадач, вместо n ( n – 1) при их независимом решении.

Выводы. Использование функционально-стоимостного анализа как метода бюджетирования обеспечивает наиболее эффективное распределение ограничений ресурсов во времени. Использование описанного метода позволило значительно уменьшить производственный цикл и увеличить конкурентоспособность продукции.

Список использованных источников:

1. Баркалов С.А. Математические основы управления проектами: учеб . п особ . / С.А. Баркалов , В.И. Воропаев, Г.И. Скелетова и др.; под ред. В.Н. Буркова. – М.: Высш.шк ., 2005. –423с.

2. Функционально-стоимостной анализ в управлении проектами наукоемких предприятий : монография / [Данченко Е.Б., Чернова Л.С., Бедрий Д.И., Погорелова Е.В., Мазуркевич А.И.]. – Днепропетровск: IMA – Press , 2011. – 237с.